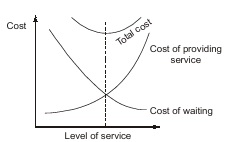
Graph of Optimization of Cost

Representation of Queueing Model

Kendalls Lee Notation:
The general form of notation is

(a/b/c ) : (d/e/f )

Here,

a = Probability distribution for arrival pattern.
b = Probability distribution for service pattern.
c = Number of servers.
d = Service rule or service order.
e = Maximum number of customers allowed in the system
f = Size of calling population.

Queueing Model 1 (M/M/1) : (FIFO/∞/∞)

M=Arrival pattern with Poisson distribution.
M=Service rate is exponentially distributed.
1 = Number of server.
FIFO = Service rule,
∞ = customer number allowed
∞ = Size of calling population

Assumption (λ < µ): : When mean arrival rate (λ) is greater than mean service rate, there will be never ending queue and it leads to queue explosion.

Remember:

In queuing model the assumption is that, if random variable is independently and identically distributed random variable then only we can assume it as Poisson distribution.