Law of Restitution

Consider two bodies of mass m1 and m2 respectively. Let these bodies be moving with respective velocities u1 and u2 before impact. The impact will take place only if u1 > u2. Thus, velocity of approach is (u1 – u2).

After a short period of contact, the bodies will separate and will start moving with velocities v1 and v2 respectively. The separation will occur only if v2 > v1 and velocity of separation is (v2 – v1).

Newton’s law of collision for elastic bodies states that

When two moving bodies collide with each other, their velocity of separation bears a constant ratio with their velocity of approach.

or v2 – v1=e(u1 – u2)

where e is a constant of proportionality and is known as coefficient of restitution. The coefficient of restitution is a parameter which indicates the energy lost during an impact. The value of e lies between 0 and 1. If e = 0, the impact is inelastic. If e = 1, the impact is perfectly elastic.

Loss of Kinetic Energy During Impact

Consider two bodies of mass m1 and m2 moving with respective velocities u1 and u2 before impact. Let v1 and v2 is their respective velocities after impact, then

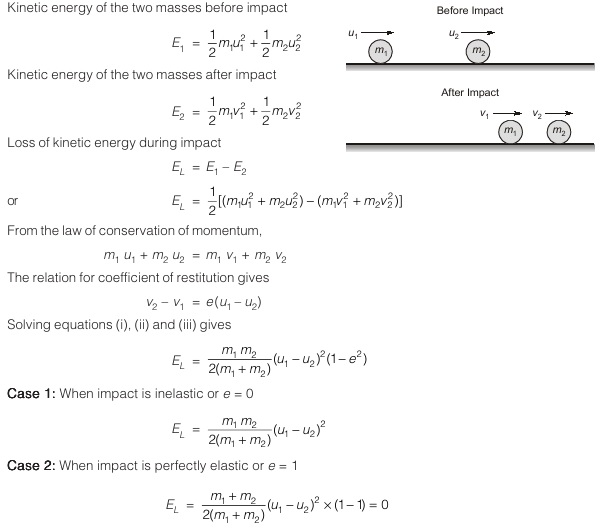
Thus, in case of perfectly elastic impact both the momentum and kinetic energy are conserved.