D’Alembert’s Principle

Introduction

D’Alembert’s Principle

In 1743, D’Alembert proved that the Newton’s second law is applicable not only to motion of particle but also to motion of body. According to Newton’s second law of motion, resultant of forces acting on a body (R) can be written as

R = ma

or it can also be written as

R – ma =0

The term –ma may be looked as a force applid in opposite direction of motion and is termed as inertia force.

D’Alembert states that the system of forces acting on a body in motion is in dynamic equilibrium with inertia force of
the body.

Consider a body as shown is subjected to a system of forces causing the body to move with an acceleration ‘a’ in the direction of resultant force. Let us apply a force equal to ma in reversed direction of acceleration. Now according to D’Alembert’s principle the equation of equilibrium ΣFx = 0, ΣFy = 0 can be used for system of forces.

Work

A body undergoes some displacement under the application of applied force, then some work is said to be done on the body, work is equal to the force multiplied by the distance traveled in the direction of the force.

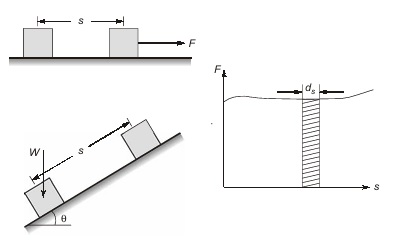
Consider a force F acting on the block placed on horizontal plane. Block moves by distance s under this force, then the work done is

U= F × s

In second case, block moves by distance along the inclined plane due to its weight, then work done by its weight is  U= W (s sinθ)

Here the displacement in the direction of force is s·sin θ. The unit of work is Nm as unit of force Newton is multiplied by unit of displacement meter. Unit of work is Joule also.

1 J = 1 Nm

Work done by varying force:

Let a varying force acting at any instant on a particle be F. Now if the particle moves a small distance ds, then work done by force is Fds. Work done by force in moving body by a distance s is ΣFs. Thus, if a force versus displacement curve is drawn, the area under curve gives the work done by force. If variation of F is in regular fashion then,
ΣFs = ∫Fds