Economic Order Quantity (EOQ)

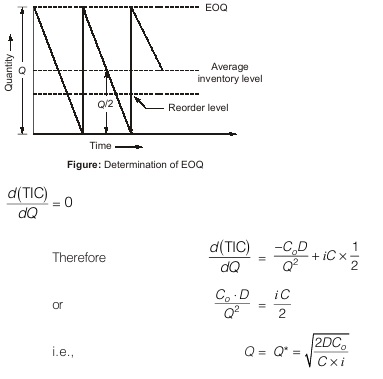
In a continuous, or fixed-order quantity system, when inventory reaches a specific level, referred to as the reorder point, a fixed amount is ordered. The most widely used and traditional means for determining how much to order in a continuous system is the economic order quantity (EOQ) model, also referred to as the economic lot-size model. The earliest published derivation of the basic EOQ model formula in 1915 is credited to Ford Harris, an employee at Westinghouse. The function of the EOQ model is to determine the optimal order size that minimizes total inventory costs. Economic order quantity is that order quantity which will minimize the total variable cost of managing the inventory.

Method of calculation of EOQ:

Assuming that the inventory decreases at a constant rate from the order quantity ‘Q’ to zero and then replenished by another quantity.

D = Annual demand/consumption of the product (units)
Co = Cost of placing an order
Cu = Unit cost of an item (unit price `)
Q = Order quantity (Units)
i = Interest rate charged per unit per year.

(Inventory carrying cost expressed as a percentage of average inventory investment).

Now, the total variable cost of managing the inventory per year

= Annual ordering cost + Annual cost of carrying the inventory = E (Say)

Therefore, TIC=[No. of orders per year] × [Cost of placing an order] + [Average Inventory] × [Inventory carrying cost]

To determine economic order quantity (Q*) that minimizes the total cost of managing the inventory, we must differentiate TIC with respect to decision variable Q and set the first derivative to zero, i.e., for minimum total cost,