MUTUAL INDUCTANCE
When we defined inductance, we did so by specifying the relationship between the terminal voltage and current,
The physical basis for such a current-voltage characteristic rests upon two things:
- The production of a magnetic flux by a current, the flux being proportional to the current in linear inductors.
- The production of a voltage by the time-varying magnetic field, the voltage being proportional to the time rate of change of the magnetic field or the magnetic flux.
Coefficient of Mutual Inductance
Mutual inductance results from a slight extension of this same argument. A current flowing in one coil establishes a magnetic flux about that coil and also about a second coil nearby. The time-varying flux surrounding the second coil produces a voltage across the terminals of the second coil. This voltage is proportional to the time rate of change of the current flowing through the first coil. Figure shows a simple model of two coils L1 and L2, sufficiently close together that the flux produced by a current i1(t) flowing through L1 establishes an open circuit voltage V2(t) across the terminals of L2.
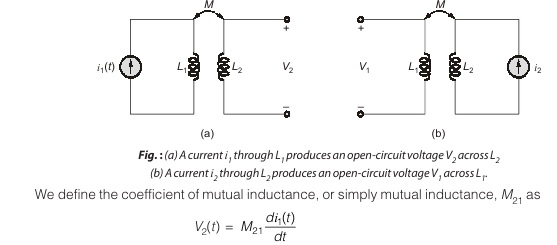
The order of the subscripts on M21 indicates that a voltage response is produced at L2 by a current source at L1. If the system is reversed, as indicted in fig. then we have
Two coefficients of mutual inductance are not necessary, however we will use energy relationship a little later to prove that M12 and M21 are equal. This M12 = M21 = M.
The existence of mutual coupling between two coils is indicated by a double-headed arrow, as shown in figure (a) and (b).
Note: It is important to know that mutual coupling exist only when the inductors are placed close to each other and input excitation is time varying.
Dear Aspirants,
Your preparation for GATE, ESE, PSUs, and AE/JE is now smarter than ever — thanks to the MADE EASY YouTube channel.
This is not just a channel, but a complete strategy for success, where you get toppers strategies, PYQ–GTQ discussions, current affairs updates, and important job-related information, all delivered by the country’s best teachers and industry experts.
If you also want to stay one step ahead in the race to success, subscribe to MADE EASY on YouTube and stay connected with us on social media.
MADE EASY — where preparation happens with confidence.
MADE EASY is a well-organized institute, complete in all aspects, and provides quality guidance for both written and personality tests. MADE EASY has produced top-ranked students in ESE, GATE, and various public sector exams. The publishing team regularly writes exam-related blogs based on conversations with the faculty, helping students prepare effectively for their exams.
