Fourier Transform
INTRODUCTION
In the previous chapter, we saw that Fourier series can be generalized only for periodic signals not for aperiodic one i.e. any periodic signal is represented as linear combination of hormonally related complex exponentials.
This limitation is overcome through Fourier transform which is applicable for both aperiodic and periodic signals. The Fourier transform gives a frequency domain description of time domain signal. An aperiodic signal is one which is periodic with an infinite period. As the period increases the fundamental frequency decreases which makes aperiodic signal infinitesimally close in frequency and the representation in terms of linear combination takes the form of an integral rather than sum. The resulting spectrum is called Fourier transform. Thus Fourier transform is extension of Fourier series for aperiodic signals.
THE DEFINITION
Consider a continuous time signal x(t). Its Fourier transform is defined as

Conditions for existence of Fourier Transform
(i) Signal x(t) should be absolutely integrable. i.e.,

(ii) Signal x(t) should be deterministic over any finite interval.
(a) It should have finite number maxima and minima over a finite interval.
(b) It should have finite number of finite size discontinuities over finite interval.
The conditions are sufficient not necessary. It means that there is class of signals that violate either one or both conditions, possess Fourier transform.
e.g. power signal, periodic signals. etc.
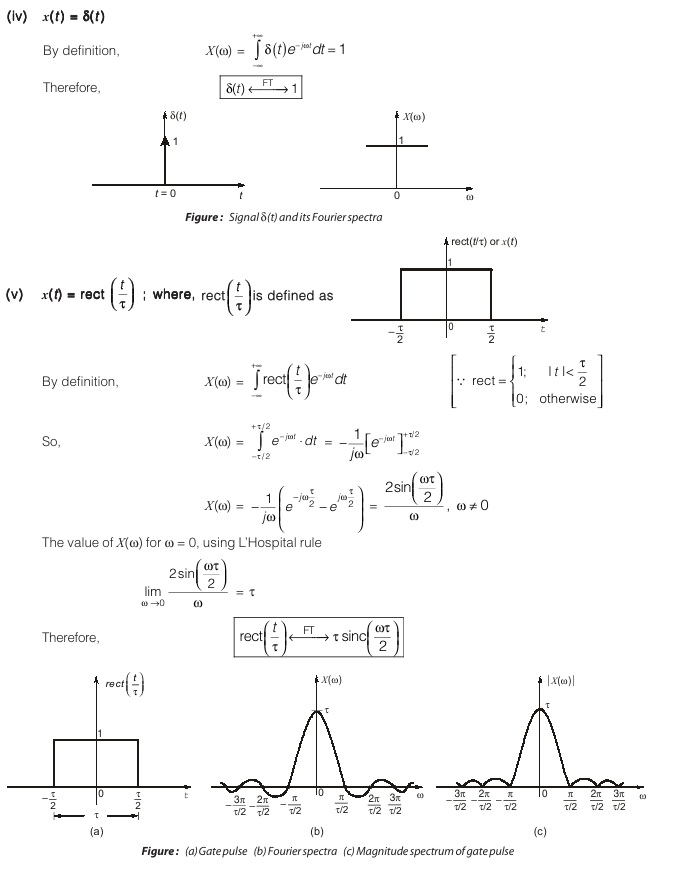
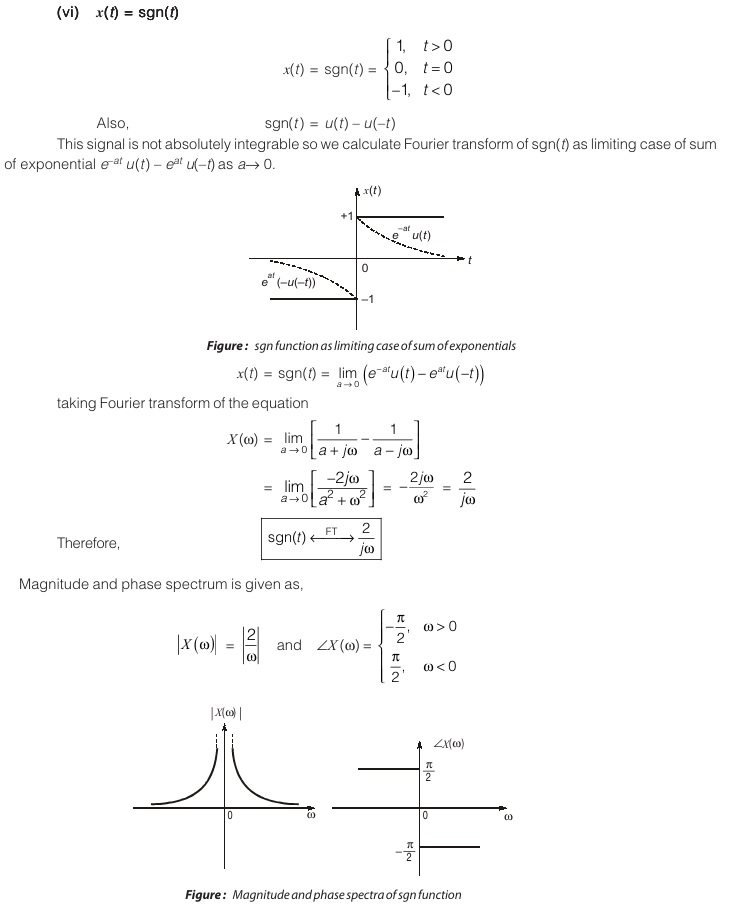
FOURIER TRANSFORM OF SOME BASIC SIGNALS
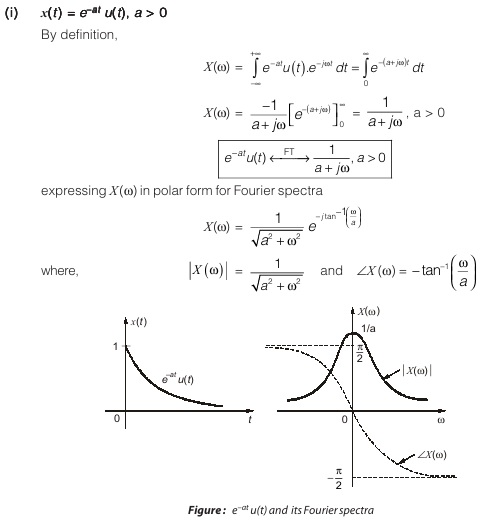
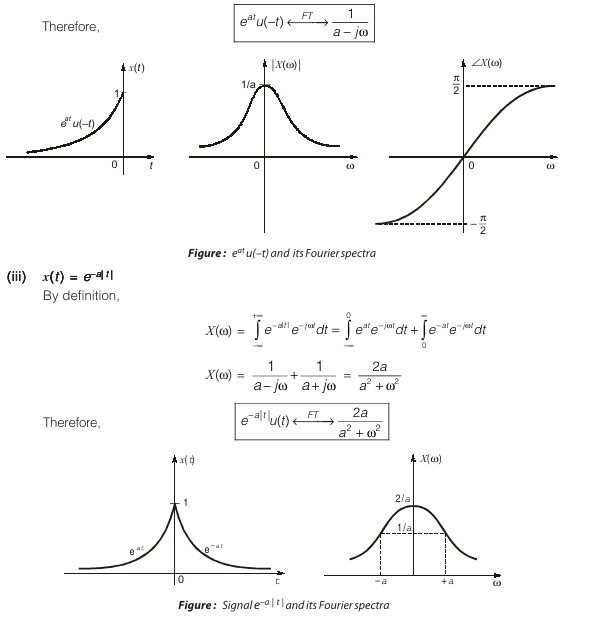
Observing |X (ω)| and ∠X (ω), we see magnitude spectrum |X (ω)| is even function of ω and phase spectrum ∠X (ω) is an odd function of ω.