z-Transform

The discrete-time counterpart of Laplace transform is z-transform. The frequency domain analysis of discrete time system allows us to represent any arbitrary signal x[n] as a sum of exponential of the form zⁿ.
There are two varieties of z-transform: bilateral and unilateral. The bilateral one, also known as two- sided z-transform.
can handle all causal and non causal signals. It provides insights about system’s characteristics such as stability, causality and frequency response.

The unilateral one, also known as one-sided z -transform can handle only causal signals and mainly used to solve
difference equations with initial conditions.
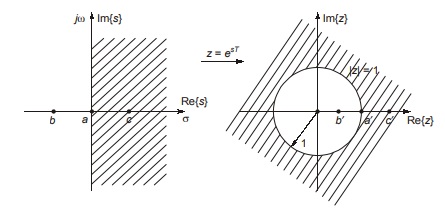
The purpose of the z-transform is to map (transform) any point s = ±σ ±jω in the s-plane to a corresponding point z(r ∠Ω) in the z-plane by the relationship.

z = e^sT, where T is sampling period (seconds)

Under this mapping, the imaginary axis, σ = 0 maps on to the unit circle |z| = 1 in the z-plane. Also, the left half –  plane, σ < 0 corresponds to the interior of the unit circle |z| = 1 in the z-plane.

The mapping of s-plane to z-plane is shown in figure.

The Definition of z-Transform

Consider a discrete-time signal x[n]. Its z-transform is defined as

Region of Convergence for z-transform

The z-transform is guaranteed to converge if x[n] ⋅ r ^–n is absolutely summable.

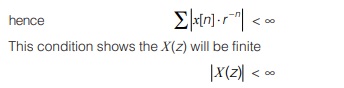
Thus, ROC consist of those values of |z| = |re^iΩ| = r for which z-transform converges.

Properties of ROC

1. The ROC of (i) X(z) consists of a ring in the z-plane centered about the origin.
2. The ROC does not contain any poles.
3. If x[n] is of finite duration, then the ROC is entire z-plane, except possibly z = 0 and/or z = ∞.
4. If x[n] is a right-sided sequence, and if the circle |z | = r0 is in the ROC then all finite values of z for which | z | > r0 will also be in the ROC.
5. If x[n] is a left-sided sequence, and if the circle | z |= r0 is in the ROC, then all values of z for which 0 < |z |< r0 will also be in the ROC.
6. If x[n] is two sided, and if the circle | z |= r0 is in the ROC, then the ROC will consist of a ring in the z-plane that includes the circle | z |= r0.
7. If the z-transform X(z) of x[n] is rational, then its ROC is bounded by poles or extends to infinity.
8. If the z-transform X(z) of x[n] is rational and if x[n] is right sided, then the ROC is the region in the z-plane outside the outer most pole i.e., outside the circle of radius equal to the largest magnitude of the poles of X(z). Furthermore, if x[n] is causal (i.e., if it is right sided and equal to 0 for n < 0), then the ROC also includes z = ∞.
   (ix) If the z-transform X(z) of x[n] is rational, and if x[n] is left sided, then the ROC is the region in the z-plane inside the innermost non-zero pole i.e. magnitude of the poles of X(z) other than any at z = 0 and extending inward to and possibly including z = 0. In particular, if x[n] is anti-causal (i.e., if it is left sided and equal to 0 for n > 0), then the ROC also includes z = 0.

The z-plane and poles and zeros

The graphical representation of complex number z = rej^Ω in terms of complex plane is called as z-plane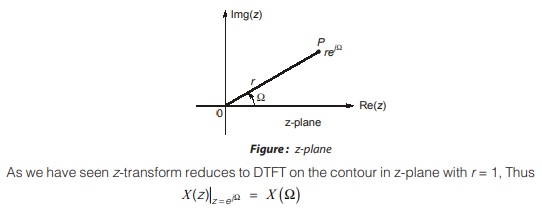

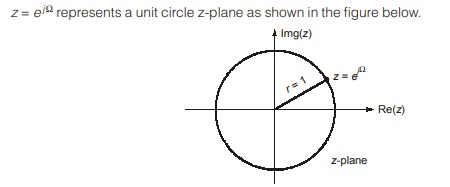
It is concluded that DTFT corresponds to z-transform evaluated on unit circle.