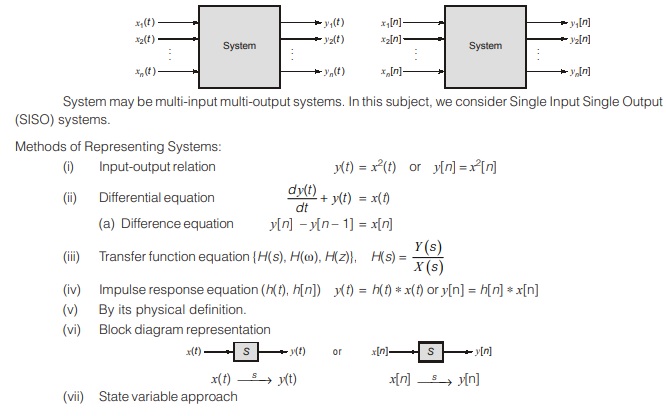
Systems

A system is an operator which maps the relation between input signal and output signal by the process of transformation. A system may also be defined as set of elements which produces expected output with available input. The examples of systems are electrical system, mechanical system, electromechanical system etc.

In brief, a system is mathematical identity which maps a set of input (x(t) or x[n]) to set of output (y(t) or y[n]).

Continuous-time and Discrete-time Systems

A continuous time system (CTS) is one in which continuous time input signals are transformed into continuous time output signals.

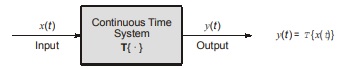
e.g. integrator, differentiator, filters etc.
A discrete time system (DTS) is one which transform discrete time input signal into discrete time output signal.

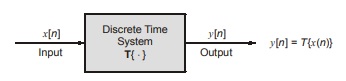
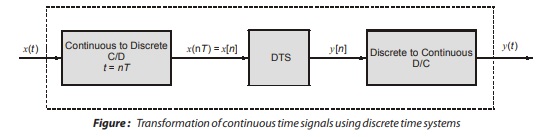
Moreover, a continuous time signal can be processed by a discrete time system. This is done, because discrete time systems have several significant advantages over continuous time systems.

Continuous-Time Fourier Series

Fourier series is an approximation process where periodic signal is expressed as sum of harmonically related sinusoids. It gives us frequency domain representation.
The representation of a non-sinusoidal periodic signal in terms of complex exponentials, or equivalently, in terms of sine and cosine waveforms, leads to the Fourier series. The Fourier series is named after the French physicist Joseph Fourier, who was the first to suggest that periodic signals could be represented by a sum of sinusoidals.

Different Forms of Fourier Series

Trigonometric Fourier Series

A periodic signal x(t) can be expressed as infinite sum of sine or cosine functions that are integral multiples of ω₀

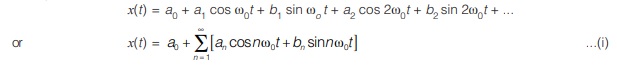
Where, ω₀ = 2π/T = is known as fundamental frequency (rad/sec) and the constant a₀, a_n and b_n are the Fourier coefficients. The coefficient ‘a₀’ is the dc component.
The process of determining the coefficients is called Fourier analysis.

The following trigonometric integrals are very useful in Fourier analysis. For any integers m and n

To find value of a₀, integrate equation (i) both sides over a period T

Similarly, we obtain b_n by multiplying both sides of equation (i) with sinmω0t and integrating over a period T, we get

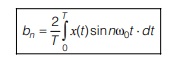
Polar Form of Trigonometric Fourier Series

Fourier series can be expressed in polar form or compact form as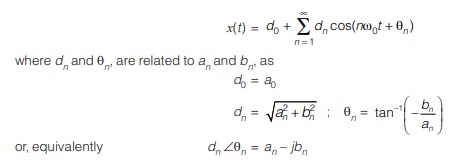
Since coefficients a_n and b_n are real so d_n and θ_n are also real are also real

Exponential Fourier Series

By using Euler’s equality, each of sine and cosine terms in the trigonometric series can be expressed in terms of exponential e^-jnω0t and e^+jnω0t as

Fourier Spectrum:

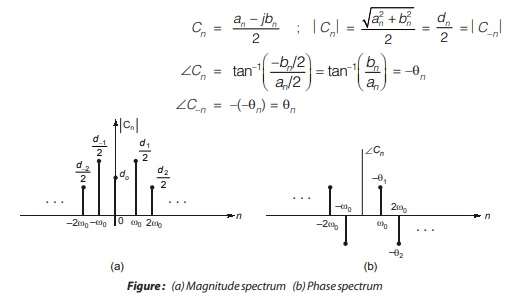
The magnitude spectrum of exponential Fourier series is even symmetric and phase spectrum is odd symmetric. Therefore, C_n is even conjugate or conjugate symmetric.

Continuous Time FOurier Transform (CTFT)

In the previous chapter, we saw that Fourier series can be generalized only for periodic signals not for aperiodic one i.e. any periodic signal is represented as linear combination of hormonally related complex exponentials.
This limitation is overcome through Fourier transform which is applicable for both aperiodic and periodic signals. The Fourier transform gives a frequency domain description of time domain signal. An aperiodic signal is one which is periodic with an infinite period. As the period increases the fundamental frequency decreases which makes aperiodic signal infinitesimally close in frequency and the representation in terms of linear combination takes the form of an integral rather than sum. The resulting spectrum is called Fourier transform. Thus Fourier transform is extension of Fourier series for aperiodic signals.

The Definition

Consider a continuous time signal x(t ). Its Fourier transform is defined as

In terms of frequency ‘f ’ (Hz), the Fourier transform equations are

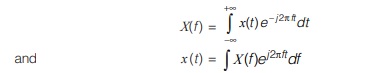
Conditions for existence of Fourier Transform

(i) Signal x(t) should be absolutely integrable. i.e.,

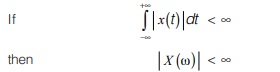
(ii) Signal x(t) should be deterministic over any finite interval.

• It should have finite number maxima and minima over a finite interval.
• It should have finite number of finite size discontinuities over finite interval.

The conditions are sufficient not necessary. It means that there is class of signals that violate either one or both conditions, possess Fourier transform.
e.g. power signal, periodic signals. etc.