Sampling

The process of sampling is a bridge between continuous-time and discrete-time domains. Sampling is a process of converting a continuous-time signal to discrete-time signal and under certain condition the continuous time signal can be completely recovered from its sampled sequence.

The Sampling Theorem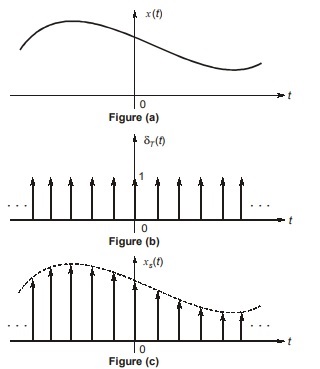

According to sampling theorem “A band limited signal of finite energy can be completely reconstructed from its samples taken uniformly at a rate ω_s ≥ 2ω_m samples/rad/sec (or, f_s ≥ 2f_m sample/sec)”.

In other words, the minimum sampling rate is
f_s = 2f_m Hz.

To prove sampling theorem, let x(t) be continuous-time finite energy signal whose spectrum is band limited to ω_m rad/sec (i.e. X(ω) = 0 for | ω | > ω_m).

The input x(t) is sampled at the rate of f_s Hz by multiplying x(t) by a periodic impulse train δ_T (t) with period T_s = 1/f_s.

The sampled signal ‘x_s(t)’ consists of impulses spaced every T_s second whose strength (area) is equal to instantaneous value of input signal x(t)

Taking Fourier transform of equation (ii) and using multiplication property of Fourier transform

The sampling frequency can take three possible values with respect to spectrum width (2 ω_m)

(i) ω_s > 2 ω_m
(ii) ω_s = 2 ω_m
(iii) ω_s < 2 ω_m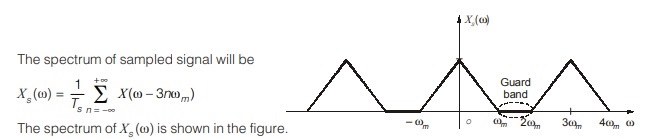

Case-1 ω> 2 ω_m

Let, ω_s = 3 ω_m

We see for ω_s > 2ω_m, there is no overlap between the shifted spectrum of X(ω). Thus, as long as the sampling  frequency ωs is greater than the twice the signal bandwidth (2 ω_m), x(t) can be recovered by passing the sampled signal x_s (t) through ideal or practical low pass filter having bandwidth between ωm and (ω_s – ω_m) rad/sec.

Case-2 ω_s = 2 ω_m

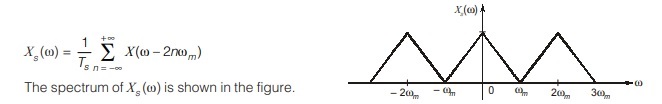
We see for ω_s = 2 ω_m , there is no overlap between shifted spectrum of X(ω). Consequently, x(t) can be recovered from its sampled signal by means of an ideal low pass filter. The minimum sampling rate ω_s = 2 ω_m (or, f_s = 2f_m) required to recover x(t) is called Nyquist rate.

Case-3 ω_s < 2 ω_m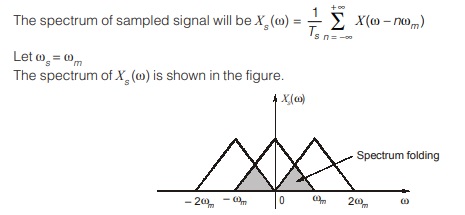

We see for ω_s < 2ω_m, there is overlap between shifted spectrum of X(ω). Consequently, the signal x(t) cannot be exactly recovered from its sampled signal.

Aliasing or Spectrum Folding

The overlap in shifted spectrum of original signal is termed as “aliasing”.
In other words, “The phenomenon of high frequency component taken on the identity of low frequency component is known as aliasing”. To avoid aliasing, the condition is ω_s ≥ 2ω_m.