Laplace Transform

In Fourier transform, one problem we faced that Fourier transform is not applicable for signals that are not absolutely integrable. This problem could be resolved by generalizing Fourier transform which leads to development
of Laplace transform. The Laplace transform can be applied to broader class of signals compared to Fourier transform and analysis of many unstable systems thus play an important role in study of stability of systems. There are two varieties of Laplace transform: bilateral and unilateral. The bilateral one, also known as two- sided Laplace transform is defined for – ∞ ≤ t ≤ ∞ can handle all causal and non causal signals. It provides insights about system’s characteristics such as stability, causality and frequency response.
The unilateral one, also known as one-sided Laplace transform can handle only causal signals and mainly used to solve differential equations with initial conditions.

The Definition of Laplace Transform

Consider a continuous time signal x (t ). Its Laplace transform (bilateral)

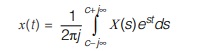
where ‘c’ is constant and responsible for convergence of integral.

Relationship between Laplace Transform and Fourier Transform

For a signal x(t), its Laplace transform X(s) is given by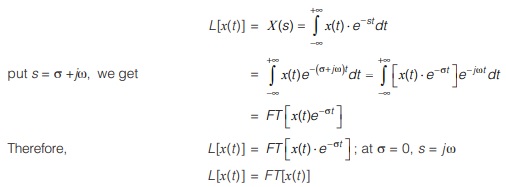

Region of Convergence (ROC) for Laplace Transform

Region of Convergence (ROC) is the set of values of ‘s’ for which the Laplace transform of the signal converges. The Laplace transform is guaranteed to converge if x(t)e^–σt is absolutely integrable

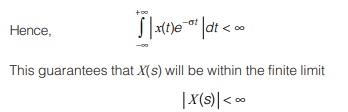
Thus ROC consist of those values of “σ” [Re {s}] for which the Fourier transform of x(t) e^–σt converges.

Properties of ROC

1. ROC along with algebraic expression of X(s) provides complete specification of Laplace transform.
2. In case of identical algebraic expression for X(s) the Laplace transforms are distinguishable only by ROC.
3. The ROC of X(s) consists of strips parallel to the jω-axis in s-plane.
4. If signal x(t) is of finite duration then the ROC is entire s-plane excluding possibly s = 0, ∞, –∞.
5. For rational Laplace transform, the ROC does not contain any poles.
6. For rational Laplace transform, if x(t) is left sided, the ROC is the region in the s-plane to the left of the left most pole and if x(t) is right sided, the ROC is the region to the right of the right most pole.
7. If ROC for X(s) includes jω axis, the Fourier transform to x(t) is possible.

The s-plane and poles and zeros

The graphical representation of complex frequency ‘s’ in terms of complex plane is called s-plane. with s = σ + jω, horizontal axis represents the real part (σ), and vertical axis represents imaginary part (jω) Consider a ratio of two polynomials, say F(s)