Discrete Time Fourier Series (DTFS)
In continuous-time Fourier series, periodic signals are represented as sum of complex exponentials. The continuous-time Fourier representation of periodic signal takes a form of infinite series whereas discrete time Fourier representation is of finite series, as a result of this, there is no convergence issue with DTFS.
The Definition of DTFS
The discrete time Fourier series representation is given as

Features of DTFS
- Fourier series representation of discrete and periodic signal is also discrete and periodic.
- Ck is periodic with ‘N’ i.e. Ck = Ck + N
- Fourier series for discrete time periodic signal is a finite sum defined entirely by the value of signal itself over one period, the series always converges.
- Ck repeats every 2π interval along Ω scale.
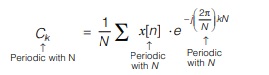
Discrete Time Fourier Transform
The extension of discrete-time Fourier series for discrete-time aperiodic signals gives discrete-time Fourier transform. The frequency domain description of discrete-time signal is continuous function of Ω that can take any
value over continuous interval from –∞ to +∞ and it is periodic function of frequency with period 2π.
The Definition of DTFT
Consider a discrete-time signal x[n]. Its discrete-time Fourier transform (DTFT) is defined as
Note:
Many books use different-different notations for frequency domain description, commonly used are X(jω), X(Ω), X(jΩ), X(e j Ω), X(e j ω). Here in this text we will use X(Ω) throughout subject.
Nature of Fourier Spectrum and Periodicity of DTFT
X(Ω), the frequency domain representation is continuous function of Ω which can take any value over a continuous interval from –∞ to +∞. Also, X(Ω) is periodic function of Ω with period of 2π. It follows that
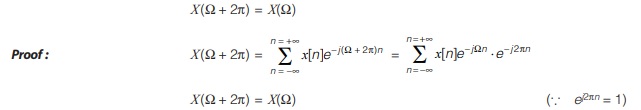
Distortionless Transmission:
In many applications it is required that the output waveform (signal) be a replica of input. Transmission is said to be distortionless if input x[n] and output y[n] satisfy the condition.
y[n] = k x[n – n0] …(i)
Where ‘k’ is a constant and accounts for scaling in amplitude and n0 accounts for the delay (in samples) is assumed to be an integer.
Taking Fourier Transform of equation (i) yields,

So for distortionless transmission, we require linear phase characteristics. The phase is not only linear function of Ω but it should also pass through Ω = 0.
In practice many systems have phase response that may be only approximately linear, thus slope varies with Ω. This variation is measured in terms of phase delay and group delay.
Phase Delay
The time delay experienced by ‘single-frequency’ signal when the signal passes through a system is referred to as phase delay and it is given as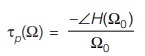
Group Delay
“The time delay experienced by group of frequencies when a input signal that contains components with different frequencies (not harmonically related) passes through a system is referred as group delay and it is given as
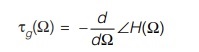
Discrete Fourier Transform
Digital processing of Fourier transform of continuous time signal x (t) requires sample values of x (t) and also a computer can compute X (f) only at some discrete values of ‘ω’. Therefore we need to relate the samples of x (t) to samples of X (f).
Consider an arbitrary signal x (t) which is time limited whose spectrum X (f) is non-bandlimited.
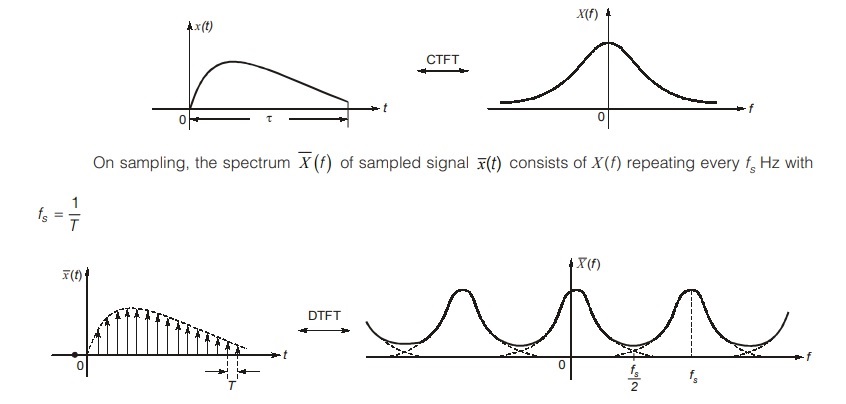
The sampled signal is repeated periodically every T0 second. According to spectral sampling theorem, such an operation results in sampling of spectrum at a rate of T0 sample/Hz with f0 = i/T0HZ.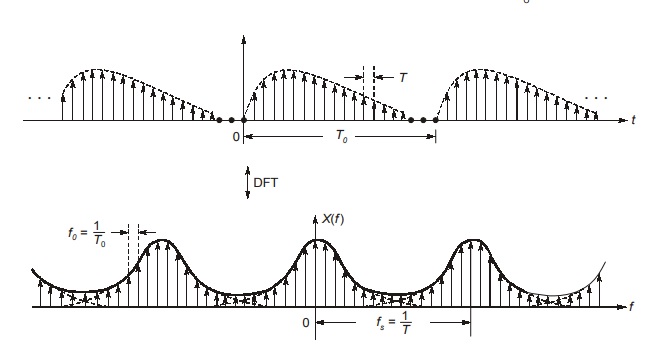
The overall operation can be viewed as when a signal x(t) is sampled and then periodically repeated, the corresponding spectrum is also sampled and periodically repeated.
The discrete Fourier transform (DFT) is basically Fourier transform of “sampled signal repeated periodically”. The number of points in DFT is known as N-point DFT.
The Definition of DFT
Consider a sampled and periodic signal x[n]. Its DFT is given as


