Network Parameters

What is Network Parameters?

A pair of terminals through which a current may enter or leave a network is known as a port. Most of the circuits we have dealt with so far are two-terminal or one-port circuits, represented in fig. (a). We have considered the voltage across or current through a single pair of terminals-such as the two terminals of a resistor, a capacitor, or an inductor. We have also studied four-terminal or two-port circuit involving op-amps, transistors and transformer as shown in fig. (b). Thus, we can say that a two-port network is an electrical network with separate ports for input and output.

In general, a network may have n ports. In this chapter, we are mainly concerned with two-port networks (or simply, two ports).

In two port network four variables are use (i.e., V₁, V₂, I₁, I₂ ) out of four variable, we can chose two variable in six different way (⁴C₂), and hence we have six sets of two-port.

• Z-parameters (Impedance parameters)
• Y-parameters (Admittance parameters)
• ABCD parameters (Transmission parameters)
• A’ B’ C’ D’ parameters (Inverse transmission parameters)
• h-parameters (Hybrid parameters)
• g-parameters (Inverse hybrid parameters)

Z-Parameters

The Z-parameter, or impedance parameters, relates current to voltage, as one would expect. The Z-parameters are 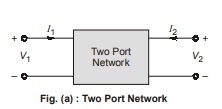the inverse of the Y-parameters in most cases.

The terminal voltage can be related to the terminal currents as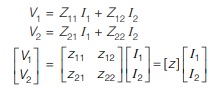

The values of the parameters can be evaluated by setting I1 = 0 (input port open-circuit) or I2 = 0. (output port open-circuited). Thus

where,

Z₁₁ = Open-circuit input impedance
Z₁₂ = Open-circuit transfer impedance
Z₂₁ = Open-circuit transfer impedance from port 2 to port 1
Z₂₂ = Open-circuit output impedance

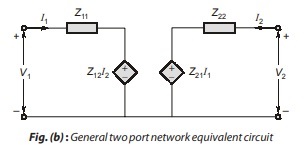
The equivalent circuit representation of equation (12.1) and (12.2) is in figure shown below, where Z₁₂ I₂ and Z₂₁ I₁ are current-controlled voltage sources (CCVS).

The equivalent circuit for equation (12.1) and (12.2) is given as

Condition of Reciprocity and Symmetry

Reciprocity network : A two port network is said to be reciprocal if the ratio of response to excitation remains the same even when there positions are interchanged.

Symmetrical Network: Network is said to be symmetrical if the ratio of current and voltage at some (one) port is same as ratio of current and voltage at other port.

Note:

For small independent networks symmetry can be identified by the “mirror image property”.

Y-parameters

In the previous section we saw that impedance parameters may not exist for a two-port network. So, there is a need for an alternative means of describing such a network. This need may be met by the second set of parameter which we obtain by expressing the terminal currents in terms of the terminal voltages.

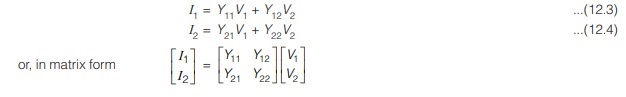
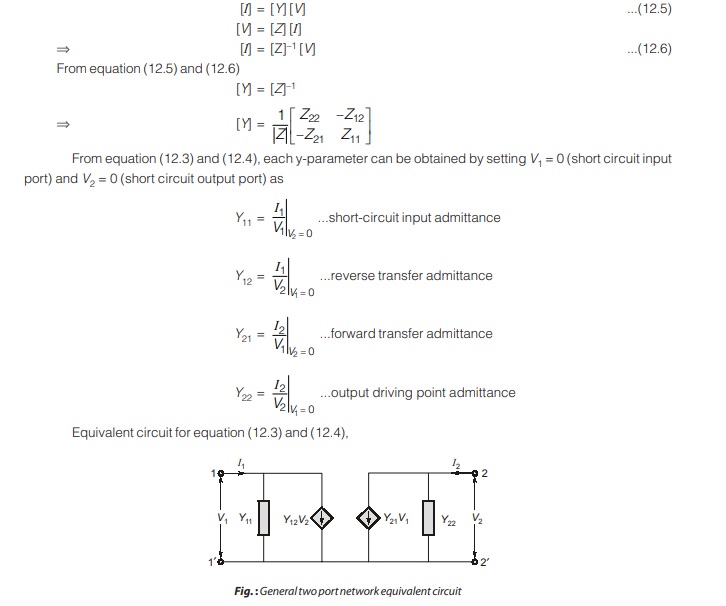
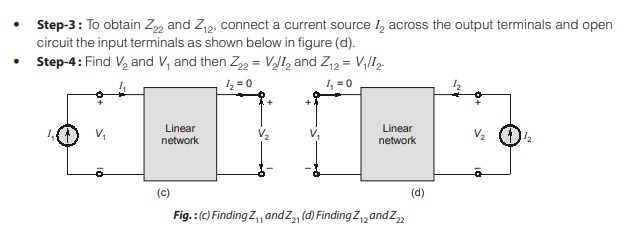
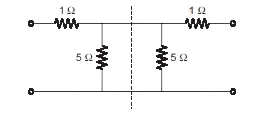
The step-by-step methodology to obtain the admittance parameters is given as following:

• Step-1 : To obtain Y₁₁ and Y₂₁, connect a voltage source V1 across the input terminals and short circuit the output terminals as shown below in fig. (a).
• Step-2 : Find I₁ and I₂ and then Y₁₁ = I₁/V₁ and Y₂₁ = I₂/V₁.
• Step-3 : To obtain Y₂₂ and Y₁₂, connect a voltage source V2 across the output terminals and short circuit the input terminals as shown below in fig. (b).
• Step-4 : Find I₁ and I₂ and then Y₂₂ = I₂/V₂ and Y₁₂ = I₁/V₂.

Condition of Reciprocity and Symmetry

For reciprocal network:

Y₁₂ = Y₂₁

For symmetrical network:

Y₁₁ = Y₂₂

Note:

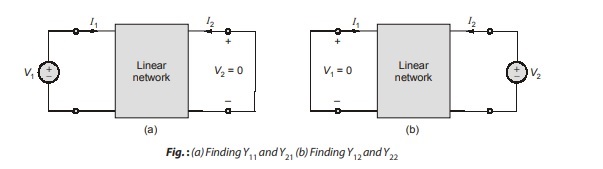
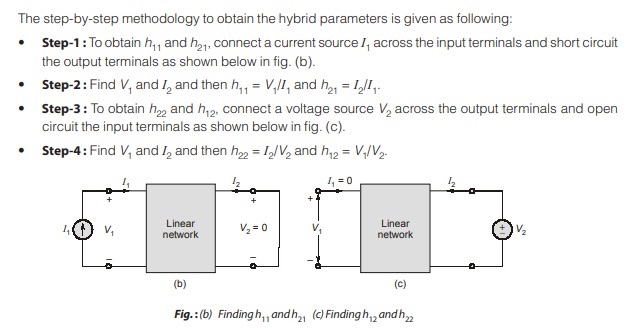
h-parameters or Hybrid Parameters

The Z and Y parameters of two-port network do not always exist. So, there is a need for developing another set of parameters. This third set of parameters is based on making V₁ and I₂ the dependent variable. Thus, we obtain h parameter which is also known as the hybrid parameters.

The hybrid parameters (h-parameters) would find wide usage in electronic circuits, especially in constructing models for transistors.

The parameters of a transistor cannot be measured either by short-circuit admittance parameter measurement or open-circuit impedance parameter measurement alone, because of the forward bias of the base emitter junction, the device has a very low input resistance. For open-circuit impedance measurement of Z₁₂ and Z₂₂, it is very difficult to make the input open circuited. Z₁₁ and Z₂₁ can be measured by open-circuit impedance measurements, since the collector-emitter junction is reversed biased.

By making a short-circuit admittance parameter measurement, Y₁₂ and Y₂₂ can be measured by short circuiting the input port, but Y₁₁ and Y₂₁ cannot be measured since the collector-emitter junction is reverse biased.

Some kind of parameter representation is required by which some parameters are measured by open circuiting the input port, while the rest of the parameters can be measured by short-circuiting the output port. This is the so-called hybrid parameter representation. This parameter representation is a hybrid of short-circuit admittance and open-circuit impedance measurement.

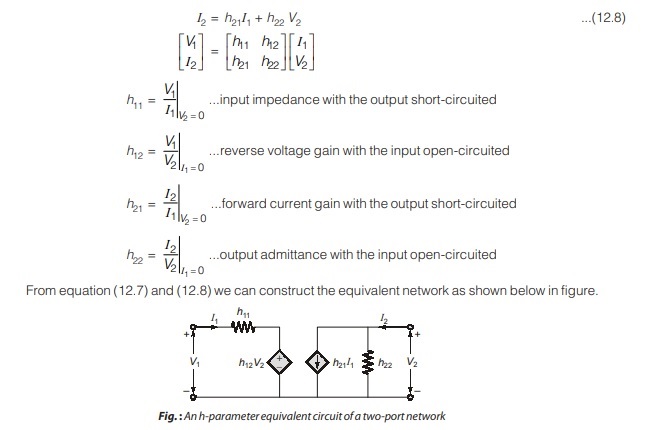
One set of equations result when the voltage of the input port and the current of the output port are expressed in terms of the current of the input port and the voltage of the output port [Refer Figure (a)], in the form

V₁ = h₁₁I₁ + h₁₂ V₂

Condition of Reciprocity and Symmetry

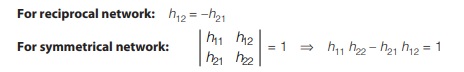
g-parameters or Inverse Hybrid Parameters

A set of parameters closely related to the h-parameters are the g-parameters or inverse hybrid parameter. These are used to describe the terminal currents and voltage as

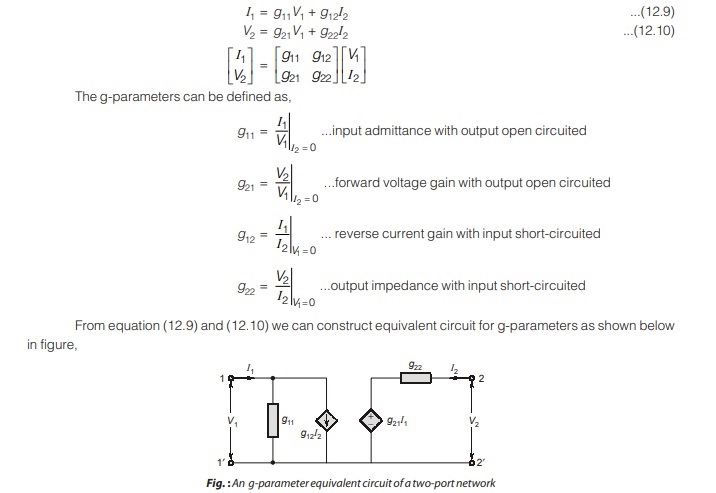
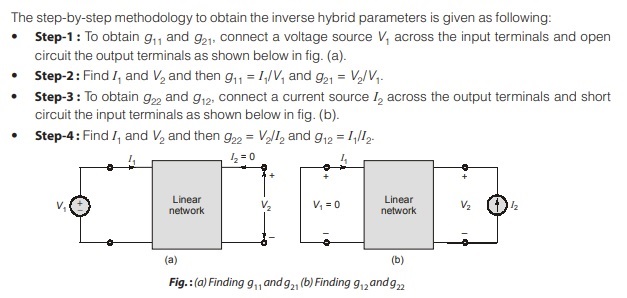
Condition of Reciprocity and Symmetry

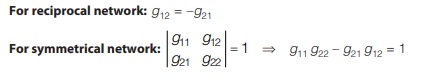
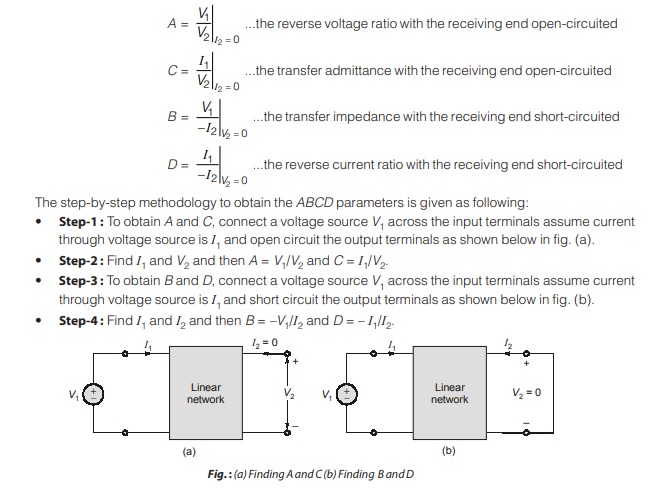
Transmission Parameters (ABCD)

Since, there are no restrictions on which terminal voltage and current should be considered independent and which should be dependent variables, we expect to be able to generate many set of parameters. Another set  of parameter relates the variable at the input port to those at the output port.

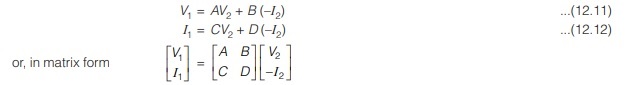
Equations (12.11) and (12.12) relate the input variables (V₁ and I₁) to the output variables (V₂ and –I₂). Notice that in computing the transmission parameter, –I₂ is used rather than I₂, because the current is considered to be leaving the network, as shown in below figure.
The transmission parameters are

Condition of Reciprocity and Symmetry

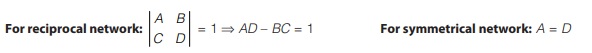
Inverse Transmission Parameters

Our last set of parameters may be defined by expressing the variables at the output port in terms of the variables at the input port we obtain

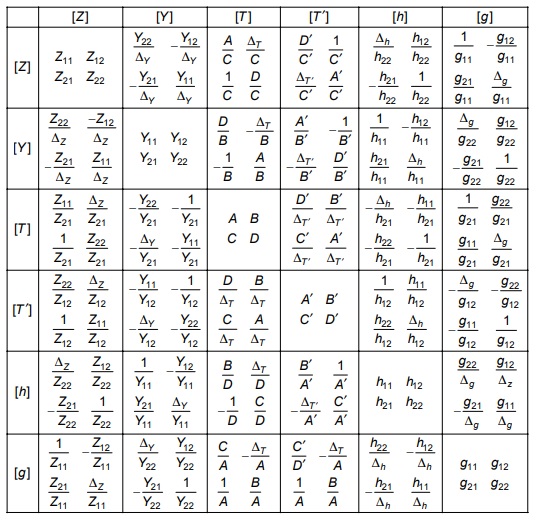
Inter Relations in Network Parameters

<< Previous | Next >>