The Nature of the Atom
In order to explain many phenomena associated with conduction in gases, metals and semiconductors and the emission of electrons from the surface of a metal, it is necessary to assume that the atom has loosely bound electrons which can be torn away from it.
Rutherford found that the atom consists of a nucleus of positive charge that contains nearly all the mass of the atom and hence it will remain substantially immobile. Surrounding this central positive core are negatively charged electrons. As a specific illustration of this atomic model, consider the hydrogen atom. This atom consists of a positively charged nucleus (a proton) and a single electron. The force of attraction between the electron and the proton follows Coulomb’s law. It can be shown from classical mechanics that the resultant closed path will be a circle or an ellipse under the action of such a force. This motion is exactly analogous to that of the planets about the sun, because in both cases the force varies inversely as the square of the distance between the particles.
Assume, therefore, that the orbit of the electron in this planetary model of the atom is a circle, the nucleus being supposed fixed in space. It is a simple matter to calculate its radius in terms of the total energy W of the electron. The force of attraction between the nucleus and the electron is e2/4π ∈0 r2, where the electronic charge e is in Coulombs, the separation r between the two particles is in meters, the force is in Newton, and ∈ 0 is the permittivity of free space. By Newtons’s second law of motion, this must be set equal to the product of the electronic mass m in kilograms and the acceleration v2/r toward the nucleus, where v is the speed of the electron in its circular path, in meters per second

which gives the desired relationship between the radius and the energy of the electron. This equation shows that the total energy of the electron is always negative. The negative sign arises because the potential energy has been chosen to be zero when r is infinite. This expression also shows that the energy of the electron becomes smaller (i.e., more negative) as it approaches closer to the nucleus.
However, an accelerated charge must radiate energy, in accordance with the classical laws of electromagnetism. If the charge is performing oscillations of a frequency f, the radiated energy will also be of this frequency. Hence, classically, it must be concluded that the frequency of the emitted radiation equals the frequency with which the electron is rotating in its circular orbit.
But if the electron is radiating energy, its total energy must decrease by the amount of this emitted energy. As a result the radius r of the orbit must decrease, in accordance with Equation above. Consequently, as the atom radiates energy, the electron must move in smaller and smaller orbits, eventually falling into the nucleus. Since the frequency of oscillation depends upon the size of the circular orbit, the energy radiated would be of a gradually changing frequency. Such a conclusion, however, is incompatible with the sharply defined frequencies of spectral lines.
The Bohr Atom
Above difficulty was resolved by Bohr. He postulated the following three fundamental laws:
- Not all energies as given by classical mechanics are possible, but the atom can possess only certain discrete energies. While in states corresponding to these discrete energies, the electron does not emit radiation, and the electron is said to be in stationary or non-radiating, state.
- In a transition from one stationary state corresponding to a definite energy W2 to another stationary state, with an associated energy W1, radiation will be emitted. The frequency of this radiant energy is given by
f = W2– W1/h
where h is Planck’s constant in Joule-seconds, the W ’s are expressed in Joules, and f is in cycles per second, or Hertz.
- A stationary state is determined by the condition that the angular momentum of the electron in this state is quantized and must be an integral multiple of h/2π. Thus
mvr = nh/2π
where n is an integer
Combining above equation, we obtain the radii of the stationary states, the energy level in Joules of each state is found to be
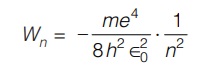
<< Previous | Next >>
Must Read: What is Electronic Devices and Circuits (EDC)?


