Mechanical Systems

All mechanical systems are divided into two parts:

1. Mechanical Translational System
2. Mechanical Rotational System

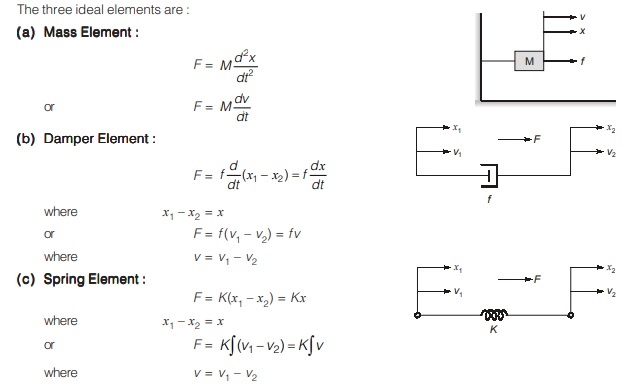
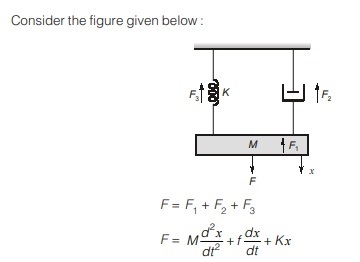
Mechanical Translational System:

Input = Force (F)
Output = Linear displacement (x) or Linear velocity (v)

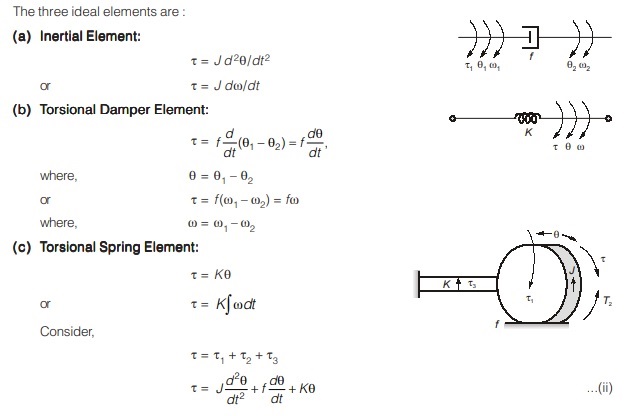
Mechanical Rotational System:

Input = Torque (τ),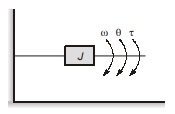
Output = Angular displacement (θ)
or Angular velocity (ω)

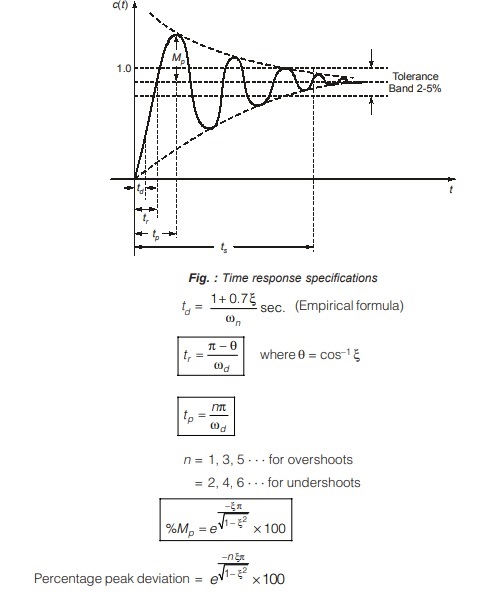
Time response of a second order (underdamped) control system subjected to unit step input function

The Routh-Hurwitz Stability Criterion (Absolute Stability)

The closed loop transfer function of a system is a ratio of two polynomials in S. The denominator polynomial of closed loop transfer function is called the characteristic equation of the system. The roots of the characteristic equation of a stable system should lie on the left of S-plane. Hence, the roots should have negative real parts.
The Routh-Hurwitz stability criterion is an analytical procedure for determine whether all the roots of a polynomial
have negative real parts or not.
The Routh-Hurwitz criterion is a method for determining continuous system stability, for systems with an nth order characteristic equation of the form:

a_n xⁿ + a_{n – 1} sⁿ – 1 + ⋅ ⋅ ⋅ a₁s + a₀ = 0

This criterion is based on ordering the coefficients of the characteristic equation into an array or table called Routh array or Routh table or Routh matrix and is defined as follows

The table is continued horizontally and vertically until only zeros are obtained.
In the process of generating Routh array, the missing terms are regarded as zero.

The Routh Stability Criterion is stated as follows :

All the roots of the characteristic equation (i.e., close loop poles) have negative real parts (i.e., they lie in left half of s-plane) so that system becomes stable, if and only if the elements of the first column of Routh array have the same sign (i.e., no sign change in first column). Otherwise, the number of roots of characteristic equation (i.e., close loop poles) with positive real parts (i.e., which lie in right half of s-plane) are equal to the number of sign changes in first column of Routh array.

• All the elements of any row can be divided by a positive constant during the process of simplifying the computational work because we are more interested to determine the sign of (first column) elements of Routh array not in their magnitudes.
• Routh array gives only the number of roots in the right half of s-plane. It gives no information regarding the values of the roots and also does not distinguish between real and complex roots.
  The following examples illustrate the applications of the Routh-Hurwitz criterion (when the tabulation terminates without complications)