Construction Rules of Root Locus

Rule-I :

Root locus is symmetrical about real axis. As Root locus is symmetrical about real axis. the poles and zeros of the open loop transfer function are either real or complex conjugate or combination of both, these are always located symmetrically about the real axis. Since the root locus starts (at K = 0) from the open loop poles and terminates (at K = ∞) either on open loop zeros or infinity. Therefore, the root locus is always symmetrical with respect to real axis (i.e. σ-axis of the s-plane). Thus, we only need to construct the upper half of the root locus and draw the mirror image of the upper half in the lower half of s-plane.

Rule-II :

Let P = Number of open loop poles and Z = Number of open loop zeros

• Case I : If P > Z
  then, the number of branches of root locus is equal to P.
  The number of branches terminating at zeros is equal to Z.
  and the number of branches terminating at infinity is equal to P – Z
  [Generally, we find that P > Z
• Case II : but if  Z > P
  The number of branches of root locus is equal to Z.
  The number of branches terminating at poles is equal to P.
  The number of branches terminating at infinity is equal to [Z – P ].

Rule-III :

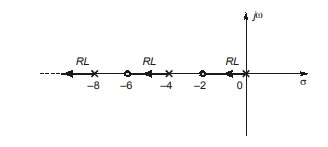
A point on the real axis lies on the root locus if the number of open loop poles plus zeros on the real axis to the right side of this point is odd i.e. root locus always lies in these regions to which the number of open loop poles plus zeros lying in right side are odd. Here, all the poles and zeros either real or complex conjugate are counted.

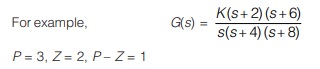
Rule-IV :

The (P – Z) branches of the root locus terminates at infinity along certain straight lines known as asymptotes
whose angles are given by

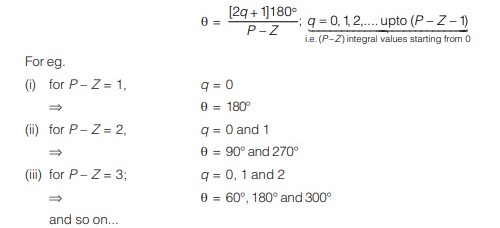
Rule-V :

Centroid: It is the point of intersection of asymptotes on the real axis. It may or may not be the part of root locus.

Rule-VI :

The breakaway points (points at which the root locus gets break) of the root locus are the solutions of dK/dS = 0.

Actually, breakaway points are the points at which multiple roots of the characteristic equation occur.

These can be determined by rewriting the characteristic equation and solving for the value of s at which dK/dS = 0.

To test valid breakaway points, put the solution of dK/dS = 0 in the expression of K (originally derived from the characteristic equation), if K comes out to be positive, the Breakaway point is valid otherwise not.

General Predictions about Break-away Points

• The branches of root locus either approach or leave the break-away point at an angle of ±180°/n where n is number of branches approaching or leaving the break-away point.
• The complex conjugate path for the branches of root locus approaching or leaving a break-away point is a circle in certain cases only.
• Whenever there are two adjacently placed poles or zeros lie on real axis (with a section of real axis between them as a part root locus) then there exists a break-away point between them.
• Whenever there is a zero on real axis and left side of that zero if these is no pole or zero on real axis with the entire section of real axis to the left side of that zero as a part of root locus then these exist a B.A. point to the left side of that zero.

Rule-VII :

The points of intersection of root locus branches with the imaginary axis can be determined by the use of Routh’s criterion. The roots of auxiliary equation A(s) at K = K_marginal will give the points of intersection of root locus with jω-axis.

Rule-VIII :

The angle of departure is obtained when the complex pole terminates at infinity. The angle of departure is tangent to the root locus at the complex pole.
The angle of departure from an open loop complex pole is given by

φD = ±180° + φ; q = 0, 1, 2,…..             where, φ = Σ(φz – φp)

where φ is the net angle contribution at this pole, of all other open loop poles and zeros.

Similarly, the angle of arrival is obtained where pole terminates at complex zero. The angle of arrival is tangent to the root locus at the complex zero. the angle of arrival at an open loop complex zero is given by

φA = ±180° – φ, q = 0, 1, 2,…..

where φ is the net angle contribution at this zero, of all other open loop poles and zeros. The angle of departure and angle of arrival are always measured from the horizontal axis.

The value of K for a particular root location so can be obtained from the actually drawn root locus plot by substituting the phasor lengths as,

[Which is basically derived from the magnitude criterion]
Here it should be noted that same scale must be employed for both the real and imaginary axis of the root locus plot in the complex s-plane.