Noise
Noise may be defined, in electrical terms, as any unwanted introduction of energy tending to interfere with the proper reception and reproduction of transmitted signals. with the proper reception and reproduction of transmitted signals Many disturbances of an electrical nature produce noise in receivers, modifying the signal in an unwanted manner. In radio receivers, noise may produce hiss in the loudspeaker output. In television receivers “snow” or “confetti” (colored snow) becomes superimposed on the picture. Noise can limit the range of the systems, for a given transmitted power. It affects the sensitivity of receivers, by placing a limit on the weakest signals that can be amplified. It may sometimes even force reduction in the bandwidth of a system. There are numerous ways of classifying noise.
- Due to sparking of brushes in electrical machinery
- Thunder and lightening
- Sparking of plugs in automobiles
- Circuit noise internal in the system
- Make-break of switches and relays
- Due to fading
- Hiss type sound in output of loudspeaker
Noise effects are of two types:
Additive Noise: When noise is added with signal.
i.e. S + N → signal deteriorates.
Fading: When noise is multiplied with signal.
i.e. S × N → signal deteriorates due to fading.
External Noise
The various forms of noise created outside the receiver come under the heading of external noise and include atmospheric, extraterrestrial noise and industrial noise.
Atmospheric Noise:
Perhaps the best way to become acquainted with atmospheric noise is to listen to shortwaves on a receiver which is not well equipped to receive them. An astonishing variety of strange sounds will be heard, all tending to interfere with the program. The majority of these radio waves come from natural sources of disturbance. They represent atmospheric noise, generally called static.
Atmospheric noise becomes less severe at frequencies above about 30 MHz because of two separate factors. First, the higher frequencies are limited to line-of-sight propagation i.e., less than 80 kilometers or so. Second, the nature of the mechanism generating this noise is such that very little of it is created in the VHF range and above.
Extraterrestrial Noise
Solar noise: The sun radiates so many things our way that we should not be too surprised to find that noise is noticeable among them only. It radiates over a very broad frequency spectrum which includes the frequencies we use for communication. However, the sun is a constantly changing star which undergoes cycles of peak activity from which electrical disturbances erupt, such as corona flares and sunspots.
Cosmic noise: Since distant stars are also suns and have high temperatures, they radiate RF noise in the same manner as our sun and what they lack in nearness they nearly make up in numbers which in combination can become significant. The noise received is called thermal (or black-body) noise and is distributed fairly uniformly over the entire sky.
Industrial noise: Between the frequencies of 1 to 600 MHz (in urban, suburban and other industrial areas) the intensity of noise made by humans easily outstrip that created by any other source, internal or external to the receiver. Under this heading, sources such as automobile and aircraft ignition, electric motors and switching equipment, leakage from high-voltage lines and a multitude of other heavy electric machines are all included.
Internal Noise
Under the heading of internal noise, we discuss noise created by any of the active or passive devices found in receivers. Such noise is generally random, impossible to treat on an individual voltage basis i.e., instantaneous value basis, but easy to observe and describe statistically. Random noise power is proportional to the bandwidth over which it is measured.
Thermal Agitation Noise
The noise generated in a resistance or the resistive component is random and is referred to as thermal agitation, White or Johnson noise. It is due to the rapid and random motion of the molecules (atoms and electrons) inside the component itself.
Noise power transferred by a resistor is directly proportional to its absolute temperature. In addition this power is also directly proportional to the bandwidth over which noise is measured.
Pn ∝ T
Pn ∝ B
Pn ∝ T B
Pn = kTB
where, Pn = noise power, T = absolute temp. (°K), B = Bandwidth (in Hz)
and k = Boltzmann constant = 1.38 × 10–23 J/K
⇒ Thermal noise is also known as Johnson’s noise.
⇒ It is also known as Gaussian noise;
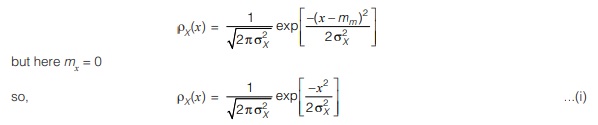
As equation (i) is a Gaussian probability density function with zero mean.
⇒ It is also known as white noise since white light contains equal amount of all frequencies within the visible band of electromagnetic radiation; similarly thermal noise has a uniform PSD over useful range of frequencies.
PSD of Thermal Noise:
Available noise power Pn = k T B
so power spectral density (PSD) = Pn/2B = kTB/2B = kT/2 W/Hz
Let us say that, η = kT,
PSD = η/2 Watt/Hz
Above equation represents two sided power spectral density of thermal noise. One sided power spectral density of thermal noise is given as
PSD(one sided) = η Watt/Hz
Shot Noise
Thermal agitation is by no means the only source of noise in receivers. The most important of all the other sources is the shot effect, which leads to shot noise in all amplifying devices and virtually all active devices. It is caused by random variations in the arrival of electrons (or holes) at the output electrode of an amplifying device and appears as a randomly varying noise current superimposed on the output.
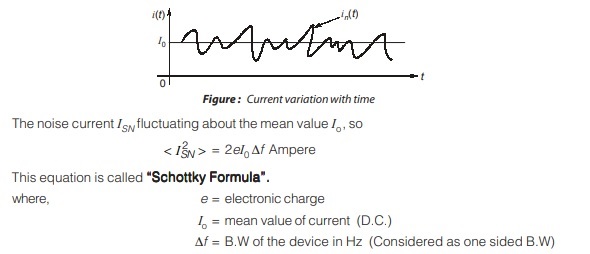
“Shot Noise” is Gaussian-distributed with zero mean. “The number of electrons contributing to the shot noise current is very large. Shot noise increases with the biasing current in a reverse biased junction and will be proportional to “I0”. This noise is negligible in FETs.
Flicker Noise/Low Frequency Noise
This noise arises due to imperfect surface behaviour of semiconductor devices and due to imperfection in cathode surface of electron tubes. The power spectral density (PSD) of this noise is inversely proportional to frequency so that it is also called (1/f) noise
PSD = S(w) a 1/f
This noise is significant at very low frequency (below few kHz).
Partition Noise
As the name occurs for this noise, it is generated in the circuit where a current has to divide between two or more paths. The partition noise results from the random fluctuations in the division.
It arises only in multi-electrode semiconductor. Hence a triode or triode transistor transistor is more transistor noisy than a diode. It has a Flat-spectrum.
Transit-Time Noise
If the time taken by an electron to travel from the emitter to the collector of a transistor becomes significant to the period of the signal being amplified, i.e., at frequencies in the upper VHF range and beyond, the so-called transit-time effect takes place and the noise input admittance of the transistor increases. The minute currents induced in the input of the device by random fluctuations in the output current become of great importance at such frequencies and create random noise (frequency distortion).
Narrowband Noise
Representation of Narrowband Noise
Canonical representation
Let n(t) represent a sample function of a NBBP noise process N(t), and npe(t) and nce(t), its pre-envelope and complex envelope respectively. We will assume fc to be the (nominal) centre frequency of the noise process.
Then, we can write:

Envelope and phase representation
Let us write n(t) as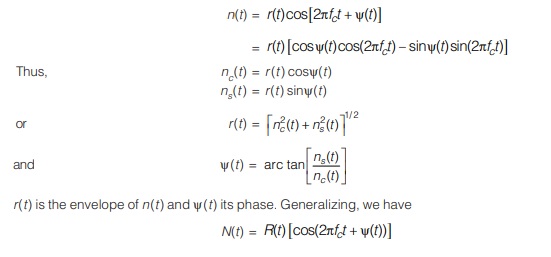
where R(t) is the envelope process and ψ(t) is the phase process. The phase equation justifies the statement that the NBN waveform exhibits both amplitude and phase variations.
Properties of narrowband noise
We shall now state some of the important properties of NBN.
Properties
If N(t) is zero mean, then so are Nc(t) and Ns(t).
If N(t) is a Gaussian process, then Nc(t) and Ns(t) are jointly Gaussian.
If N(t) is WSS, then Nc(t) and N(t) are WSS.
Both Nc(t) and Ns(t) have the same PSD which is related to SN(f) of the original narrowband noise as follows:

Given the spectrum of an arbitrary band-pass signal, we are free to choose any frequency fc as the (nominal) centre frequency. The spectral shape SNc (f) and SNs (f) will depend on the fc chosen. As such, the canonical representation of a narrowband signal is not unique.
For example, for the narrowband spectra shown in below, if f1 is chosen as the representative carrier frequency, then the noise spectrum is 2B1 wide, whereas if f2 (which is actually the mid-frequency of the given band) is chosen as the representative carrier frequency, then the width of the spectrum is 2B2 . Note for the SN(f), it is not possible for us to choose an fc such that SN(f) exhibits local symmetry with respect to it.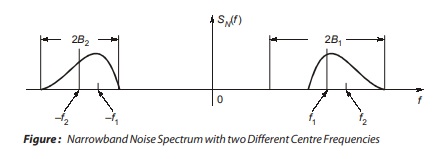
<< Previous | Next >>
Must Read: What is Communication?

