Information Theory and Coding

The basic goal of communication system is to transmit information from one point to another.

Information theory deal with efficient transmission of signals. For this some processing of the signals is to be done. Processing block is divided into two parts:

• Source coding is done in order to achieve the efficient representation of data generated by discrete source.
• Channel coding is used to introduce controlled redundancy to improve reliability.
• Source coding provides the mathematical tool for assessing data compaction that is lossless compression of data generated by discrete memoryless source. In the context of communication, information theory deals with mathematical modelling and analysis of a communication system rather than with physical sources and physical channel.

Need of Information Theory

Need of information theory can be explained with the help of following example: Ex. Horse Race.
Suppose there are 8 horses running in a race and probability of winning of horse is as specified below:

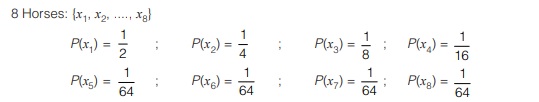
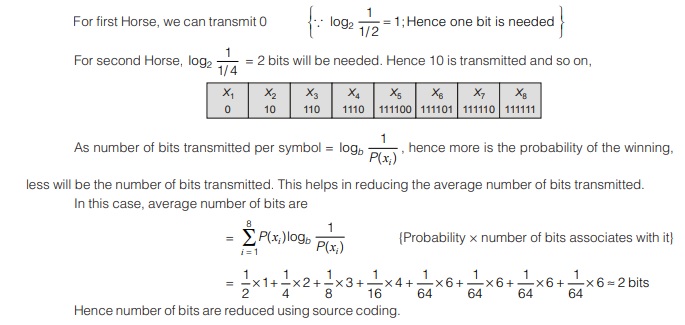
Using fixed length code, 3-bits (8 symbols) will be needed for transmission of information of winning of Horses. Now, the question arises, that if less than 3-bits can be used to transmit same information without any loss. The answer to this question is yes, by using source coding theorem.

According to source coding theorem, the number of bits transmitted for each Horse’s winning information is given by log_b 1/P(x_i), where P(x_i) probability of winning of i^th horse.

Note:

• Here b is unit, in which we measure information
  b = 10 ⇒ Information is measured in ‘Decit’ or ‘Hartley’
  b = e ⇒ Information is measured in ‘nat’
  b = 2 ⇒ Information is measured in ‘bit’
• Frequent is the event, fewer will be the bits need to transmit it, because this helps in reducing the average bit length.

According to the theorem, the number of bits per source symbol can be made as small as, but not smaller than the entropy of the source measured in bits.
Information theory provides a quantitative measure of the information contained in message signals and allows us to determine the capacity of a communication system to transfer this information from source to destination.

Information

The amount of information contained in an event is closely related to its uncertainty. Thus a mathematical measure of information should be a function of probability and should satisfy following:

(a) Information should be proportional to uncertainty of outcome.
(b) Information contained in independent outcomes should add.

Suppose that a probabilistic experiment involves observation of the output emitted by a discrete source during every signalling interval.

Entropy

In practical communication system, we usually transmit long sequences of symbols from an information source. Thus, we are more interested in the average information that the source produces rather than the information
content of a single symbol. For quantitative representation of average information, following assumptions are made:

(a) Source is stationary so that probabilities may remain constant with time.
(b) Successive symbols are statistically independent and come at average rate of r symbols/second.

The entropy of a discrete random variable, representing the output of a source of information, is a measure of the average information content per source symbol.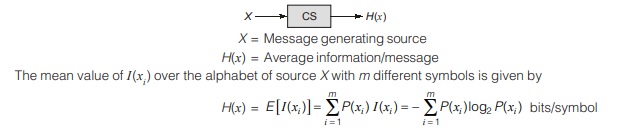

H(x) is also considered as the average amount of uncertainty within source X that is resolved by the use of alphabet.

Maximum Value of Entropy

Maximum entropy will occur when all message signals have equal probability
Let, total message signal = M
Let, each have probability = 1/M

H(x)_max = log₂ M

Entropy satisfies following relation

0 ≤ H(x) ≤ log₂M

The lower bounds corresponds to no uncertainty, which occurs when one symbol has probability P(x_i)=1 while P(x_j) = 0 for all j ≠ i, so emits the same symbol xi all the time. The upper bound corresponds to the maximum uncertainty which occurs when P(x_i) = 1/M for all i, that is, when all symbols are equally likely to be emitted by X.

Information Rate

If the rate at which source X emits symbols is r(symbols/s), the information rate R of the source is given by

Channel Capacity

Channel capacity defines the intrinsic ability of a communication channel to convey information.
Channel capacity per symbol of a DMC is defined as

where the maximization is over all possible input probability distributions {P(x_i)} on X. Note that channel capacity C_s is a function of only the channel transition probabilities that define the channel. It specify maximum number of bits allowed through channel per symbol.

Channel Capacity Per Second (C)

If r symbols are being transmitted per second, then the maximum rate of transmission of information per second is rC_s. This is the channel capacity per second and it is denoted by C(b/s):

C = rC_s | bit/sec

<< Previous | Next >>
Must Read: What is Communication?