Angle Modulation

There is another method of modulating a sinusoidal carrier wave, namely, angle modulation in which either the phase or frequency of the carrier wave is varied according to the message signal. In this method of modulation the amplitude of the carrier wave is maintained constant.

Time Domain Description of Angle Modulation

We begin our study of angle modulation by writing the modulated wave in the general form

x(t) = Acos[θ(t)]

Where the carrier amplitude A, is maintained constant, and the angular argument θ(t) is varied by a message signal m(t). In any event, a complete oscillation occurs whenever θ(t) changes by 2π radians. If θ(t) increases monotonically with time, the average frequency in hertz, over an interval from t to t +∆t, is given by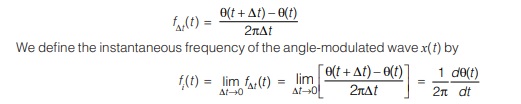 

Phase Modulation

Phase modulation (PM) is that form of angle modulation in which the angular argument φ(t) is varied linearly with the message signal m(t), as shown by

Here φ(t) ∝ m(t)
therefore, φ(t) = k_pm(t)

where, kp is the phase modulation constant with generally the unit of the radian/volts or radian/Ampere.
Now, combining the result with the carrier phase we get,

θ(t)=2πf_ct + k_pm(t)
x(t) = A_ccos [2πf_ct + k_pm(t)]

Note:

The instantaneous frequency in PM case:

ω_i(t) = d0_i(t)/dt = ω_c + k_p dm(t)/dt

f_i(t) = ω_c /2π + k_p /2π d/dt m(t)

Frequency Modulation

Frequency modulation (FM) is that form of angle modulation in which the instantaneous frequency f_i(t) is varied linearly with the message signal m(t), as shown by

f_i(t) ∝ m(t)
f_i(t) = k_f m(t)

where, k_f is the frequency sensitivity of the modulator with generally the unit of the rad/sec/volt or Hz/volt.
Now, combining the result with the carrier frequency we get,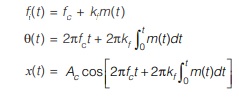

• If the units of kf is rad/sec-volt, then we write

ω_i = ω_c + k_fm(t)
f_i = f_c + k_f/2π m(t)

• If the units of kf is Hz/volt, then we write

f_i = f_c + k_fm(t)

Single-Tone Frequency Modulation

FM Modulation

Consider a sinusoidal modulating wave defined by

m(t) = A_mcos (2πf_mt)

The instantaneous frequency of the resulting FM wave equals

f_i(t) = f_c+ k_f A_m cos(2πf_mt)

= f_c + ∆f cos(2πf_mt)

where ∆f = k_fA_m

The quantity ∆f is called the frequency deviation, representing the maximum departure of the instantaneous frequency of the FM wave from the carrier frequency f_c . A fundamental characteristic of an FM wave is that the  frequency deviation frequency deviation ∆f is proportional to the amplitude of the modulating wave and is independent of the modulation fr modulation frequency.

Using the above equation the regular argument θ(t) of the FM wave is obtained as

PM Modulation

Consider a sinusoidal modulating wave defined by

m(t) = A_mcos(2πf_mt)

The instantaneous phase of the resulting PM wave equals

The quantity β is the modulation index, representing the maximum departure of the instantaneous phase of the PM wave from the carrier phase φ(t) = 2πf_c t. A fundamental characteristic of an PM wave is that the modulation index modulation index β is proportional to the amplitude of the modulating wave and is independent of the modulation fr modulation frequency.

The instantaneous frequency of the phase modulated wave can be obtained as

<< Previous | Next >>
Must Read: What is Communication?