VERTICAL CURVES

Vertical curve joins the two intersecting lines which lie in a vertical plane. e.g. Curve provided to connect two roads at the lower most point of a valley. Vertical curves are further classified as:

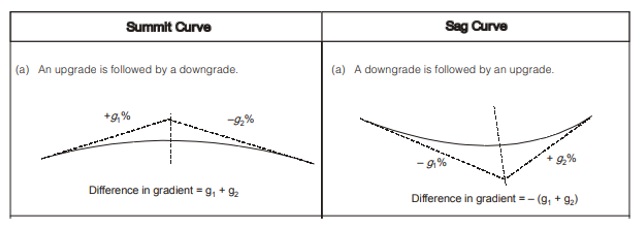
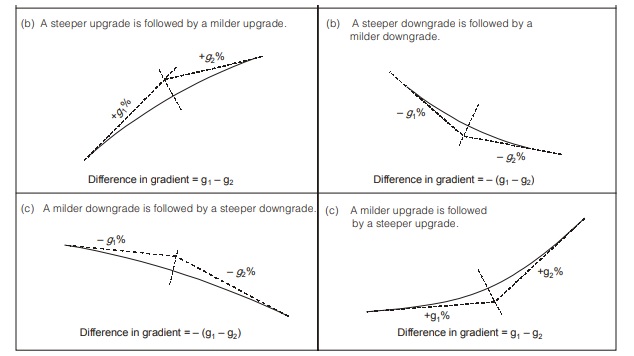
• Summit curve
• Sag curve

Summit curve and Sag curve are provided in following situations.

Degree of Curve

• The two important parameters of a circle (or the circular curve) are its center and the radius.
• Often the center of the curve which is to be laid out on a highway or for a railway is inaccessible and in such cases, the radius of the curve has no importance.
• In order to set out a curve in such situations, we define the degree of curve. This degree of curve is defined either on the basis of arc or the chord.
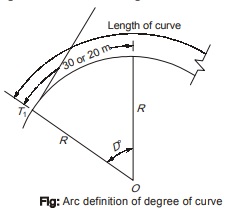
• Arc definition of degree of curve: According to this, the degree of curve is the central angle subtended by an arc of length 20 m or 30 m as the case may be.

Let     R = Radius of the curve

D = Degree of the curve as per arc definition for a 30 m arc length i.e. a 30 m arc length subtends an angle of D° at the center.

• Chord definition of degree of curve: According to this, the degree of curve is the central angle subtended by a chord of length 20 m or 30 m as the case may be.

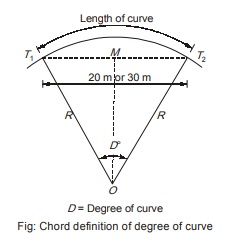
Let     R = Radius of the curve
D = Degree of the curve as per chord definition for a 30 m chord length i.e. a 30 m chord length subtends an angle of D° at the center.

Angular Methods of Setting a Simple Circular Curve

• Rankine’s method of deflection angle
• Two theodolite method
• Tacheometric method

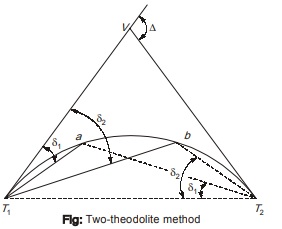
Rankine’s Method of Deflection Angle

• In this method, tape is used for making linear measurements and a theodolite is used for making angular measurements. This method is also known as tape and theodolite method.
• This method is quite suitable for setting out a circular curve of large radius and large length.
• From geometric theorem on circle, the deflection angle to any point on curve is the angle subtended at the PC (T₁) between the tangent and the chord from PC to that point. This deflection angle is one- half of the angle subtended by the arc at the center.

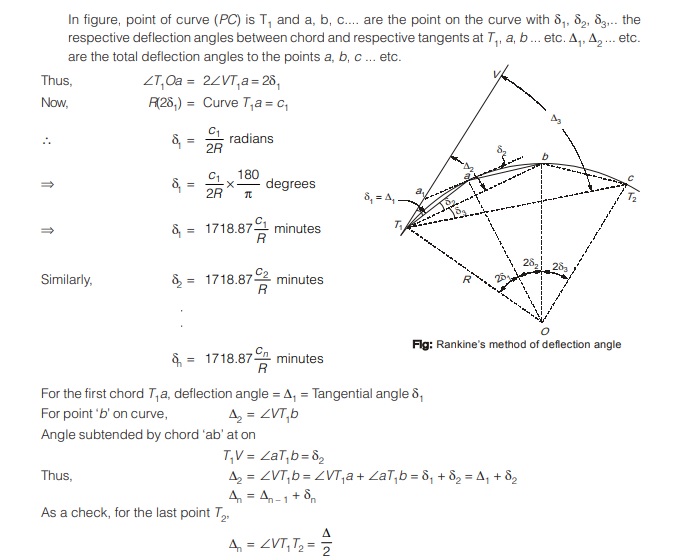
Two Theodolite Method

• It is the most preferred method of setting out a circular curve when the ground is undulating, rough and is also not suitable for the linear measurements.
• In this, no linear measurements are done. Instead two theodolites are used which gives more precision. It is based on the principle that:
  “The angle subtended by a tangent and a chord at a point on a circle is equal to the angle subtended by the chord in the opposite segment.”

Procedure:

Step 1. Set up the theodolite at point of curve, T₁ and other theodolite at point of tangent, T2.

Step 2. Set the Vernier A of both the theodolites to zero.

Step 3. Direct the theodolite at T₁ towards V and theodolite at T₂ towards T₁.

Step 4. Set angle d₁ in both the theodolites so as to direct the line of sights towards T₁a and T₂a thereby locating the point ‘a’ on the curve. The point ‘a’ is the point of intersection of the two lines of sight.

Step 5. Similarly establish point ‘b’ by setting an angle d₂ in both the theodolites.

Step 6. Repeat the above steps with different values of d to get different points on the curve.

Drawback : It is expensive and time consuming but at the same time it is the most precise method as well. All the points are established independently and thus error in locating a particular point is not carried forward to other points.

Tacheometric Method

• This method is very similar to Rankine’s method of deflection angle.
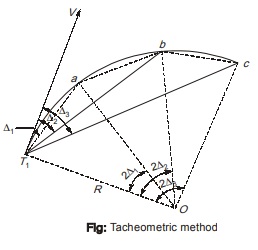
• The theodolite at T₁ is used as a tacheometer and tacheometric observations are made.
• It is less precise than Rankine’s method but here in this method, the chaining operation is completely eliminated.
• Point on the curve is established by setting the deflection angle in the tacheometer and measuring the distance of the point on the curve by placing a staff on it.
• The points a, b, c,….. So obtained are joined by T₁ and the chord lengths are given by:

<< Previous | Next >>
Must Read: What is Surveying?