Transformation Equations for Plane Strain

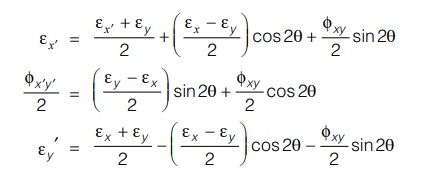
Principal Strains

These are strains on planes on which shear strains vanishes and values of shear strains are maximum and minimum. The planes are known as principals planes.

Expression for principal strain

ε₁/ε₂ = ε_x + ε_y /2 ± √ (ε_x – ε_y/2)² + (φ_xy/2)²

Angle of orientation for principal plane,

tan 2θ_p = φ_xy /ε_x – ε_y

STRAIN ROSETTE

Strain rosette is an arrangement of three linear strain gauges in which linear strains are measured in any three directions.
If among the three strains gauges two of them are mutually perpendicular then it is called rectangular rosette

If all three strain gauges are at equal angle from each other, then it is called delta ( delta (∆) rosette.

Case I: Rectangular Rosette

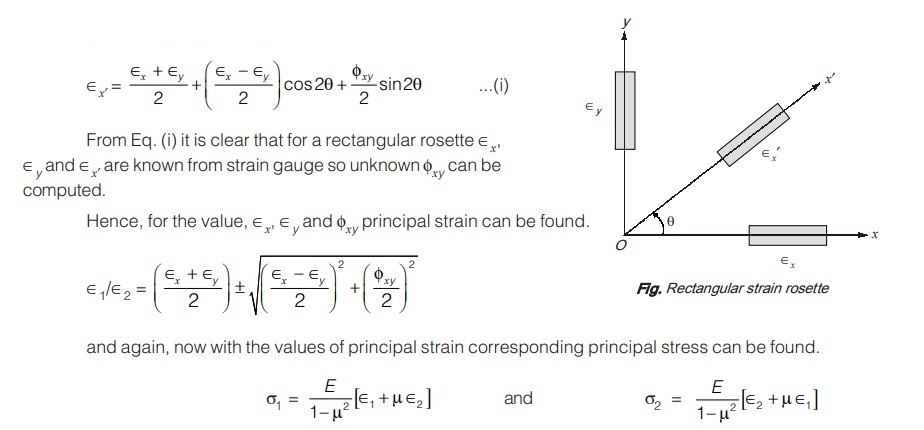
Special case 1:

If  θ = 45°

then ∈_x = ∈_o

∈_y = ∈₉₀

and ∈_x’= ∈₄₅

So, Eq. (i) can be written as

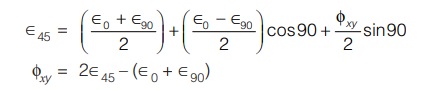
Case II: Delta (∆) Rosette

Let ∈_y is normal strain along y-direction and φ_xy is shear strain in x-y plane.

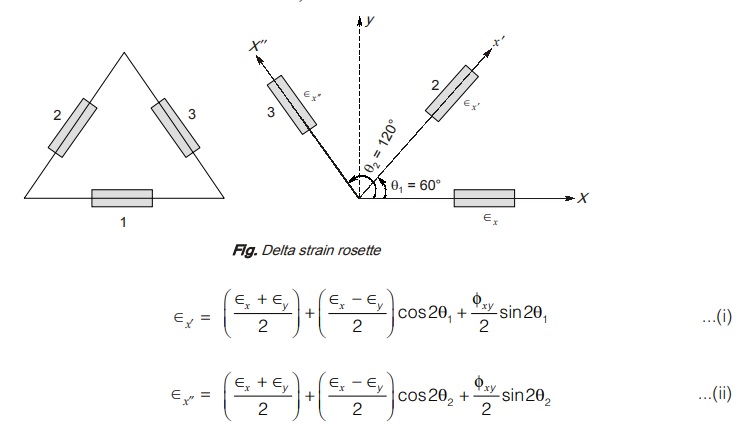
From Eq. (i) and (ii) ∈_y and φ_xy can be calculated.
Hence, ∈₁ and ∈₂ can be calculated as

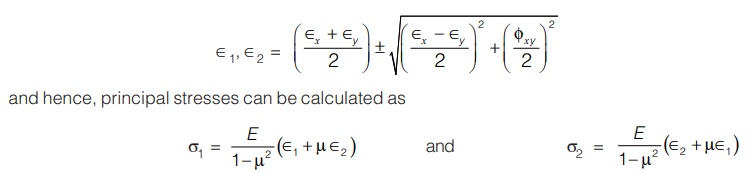
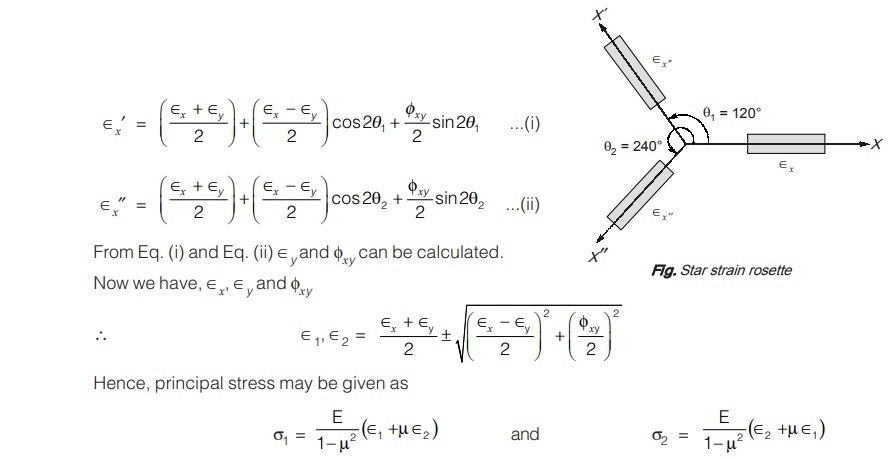
Case III: Star Rosette

Star rosette is special case is which all three strain gauges remainat an angle 120° from adjacent strain gauge.

THEORIES OF ELASTIC FAILURE

As we know a material is said to be failed if elastic limit is exceeded or permanent deformation takes place i.e., when the elastic limit is reached or when material starts yielding. In tensile test, yield stress (design stress) can be easily determined but if member is subjected to various complex stresses then it is very difficult to know the point of yielding or fracture. So, to improve the design of machine component, various theories of failure are developed considering physical behavior of material.

Generally, there are two modes of failure:

1. Yielding or ductile failure
2. Brittle failure or fracture failure

Maximum Principal Stress Theory (Rankine’s Theory)

According to this theory, the material subjected to complex stresses will fail when principal stress induced in material reaches to yield stress

σ₁ = σ_y … for tension

and failure can occur in compression when least principal stress σ3 reaches the elastic limit stress (i.e., yield stress) in compression.

σ₃ = σ_y … for compression

For no failure, maximum principal stress developed in strained material should be less than equal to yield stress in uniaxial loading

σ₁ ≤ σ_y

For design stress, suitable factor of safety is introduced.

So design stress σ_1d ≤ σ_y/FOS

• If σ_y (tension) = σ_y (compression) then this theory may be represented graphically as
• Failure will take place if any point having coordinate (σ₁, σ₂) falls outside the failure envelope.

Limitation:

• This theory neglect the effect of minor and intermediate principal stress.
• This theory is not suitable for ductile materials.
• Results of this theory are not suitable during hydrostatic loading.
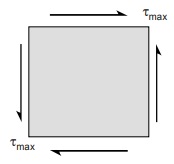
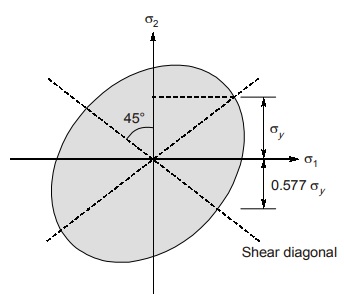
• When material is subjected to pure shear, results for ductile materials are unsafe.

σ₁ = +τ_max

σ₂ = -τ_max

According to this theory,

σ₁ ≤ σy

∴ τ_max ≤ σ_y

But experiment results show failure occurs much earlier

when τmax = 0.57 σ_y

So, for no failure in ductile material under pure shear, τ_max should be

τmax ≤ 0.57 σ_y

Maximum Principal Strain Theory (St. Venant’s Theory)

According to this theory, failure occurs when maximum strain (principal strain) in the complex stress system equals to the yield strain under uniaxial loading.

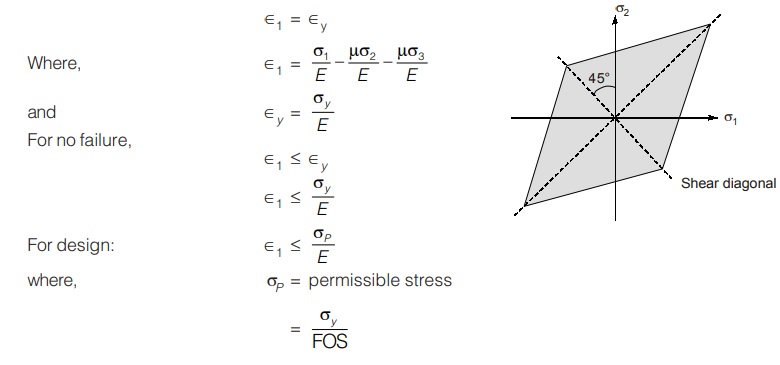
This theory can be applied for ductile and brittle materials both but results are not accurate for either case.

Limitations:

• In hydrostatic loading the results are not accurate.
• In case of pure shear, results are still unsafe for ductile materials but better than maximum principal stress theory.

Maximum Strain Energy Theory (Haigh and Beltrami)

According to this theory, failure occurs when maximum strain energy in complex stress system equals to the strain energy developed at yield stress in uniaxial loading.

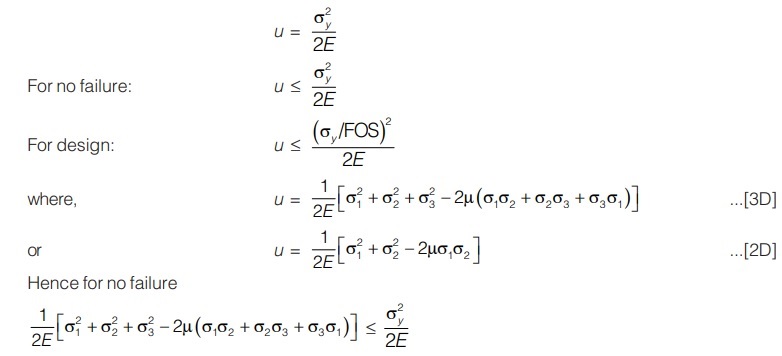
• It is suitable for ductile material.
• This theory can be graphically represented as Figure.

Limitations:

• This theory cannot be applied for brittle materials for which elastic limit stress in tension and compression are quite different.
• In case of pure shear, results are still unsafe for ductile materials.

Maximum Shear Strain Energy Theory or Distortion Energy Theory (Mises-Henky Theory)

According to this theory, failure occurs when maximum shear strain energy stored in complex stress system equals to the shear strain energy stored at yield stress in uniaxial loading.

u_s = u_ys

where u_s = shear stress energy stored due to complex stresses
and u_ys = shear strain energy stored due to yield stress
We know, total strain energy = volumetric strain energy + shear strain energy

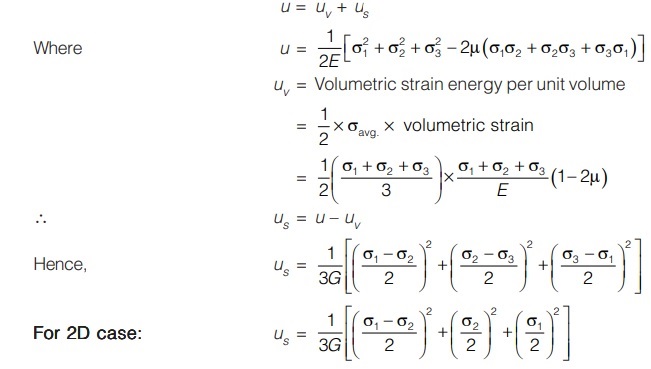
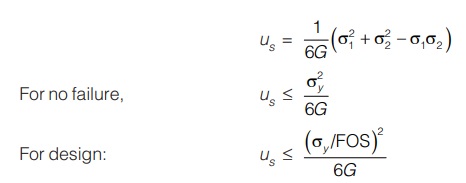
<< Previous | Next >>
Must Read: What is Strength of Material?