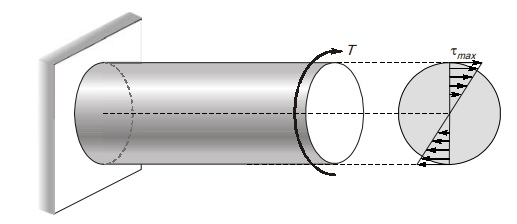
Shear Stress Distribution in Circular Section

Solid circular shaft

Hollow circular shaft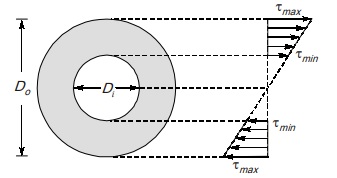

D_i = internal diameter
D_o = outer diameter

Thin circular tube with mean radius R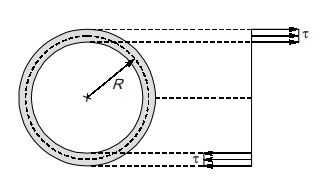

Let t is thickness of tube

I_P = Ar²
A = (2πR) × t

I_P = (2πRt)R² = 2πR³t

Z_P = I_P/R_max = 2πR³t/ R = 2πR²t

The shear stress distribution is assumed uniform across the thickness and is given by

τ = T/Z_P

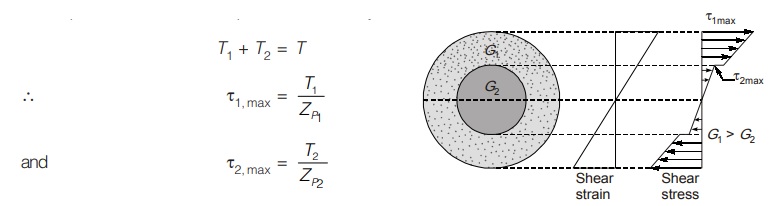
Composite circular shaft

Consider a composite circular shaft made from two materials whose modulus of rigidity are G1 and G2 In composite shaft, total torque T is shared by both shaft.

DESIGN OF SHAFT

Shaft is designed on the basis of following two criteria,

Strength criteria

τ≤τ_P

where, τ_P is permissible shear stress, τ is given as,

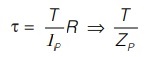
Stiffness criteria

θ≤θ_P

where, θ_P is permissible angle of twist.

Where, θ is given by,

T/I_P = Gθ/L

θ = TL/GI_P

The diameter of shaft will be greater value that is calculated by strength criteria or stiffness criteria.

SERIES COMBINATION OF SHAFT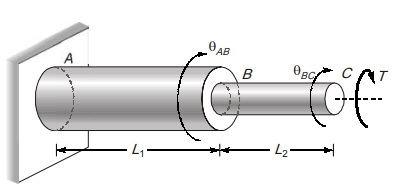

Series combination of shafts is done to transmit torque from one shaft to another shaft. For series connection couplings are used. Torque in all shaft connected in series will be equal.

T₁ = T₂ = T

Total angle of twist from A to C

θ_AC = θ_AB + θ_BC

θ_AC = TL₁/G₁I_P1 + TL2/G₂I_P2

PARALLEL COMBINATION OF SHAFT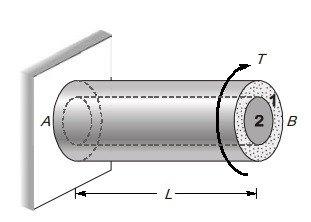

When one shaft is inside the other shaft, then two shafts are said to be connected in parallel. Parallel combination is done by providing keys between the shafts.

Let I_P1 and G₁ are properties of outer shaft and I_P2 and G₂ are properties of inner shaft.

Since there is no relative motion between them. Then angle of twist in both shaft will be equal.

θ₁ = θ₂

T₁L/G₁I_P1 = T₂L/G₂I_P2

The total torque is shared by both shafts. Hence

T₁ + T₂ = T

STRAIN ENERGY IN TORSION

The torsional strain energy of a shaft is equal to the work done in twisting

U = 1/2Tθ

where, T = Applied torque, θ = Angle of twisting

Due to torque, shear stresses are developed in metal. Hence strain energy due to torque can be represented in terms of shear stress.

Strain energy per unit volume = τ²/2G

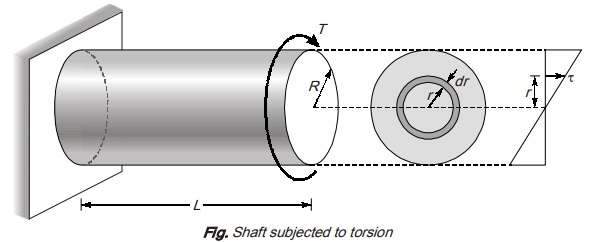
Consider a elemental tube of radius r and thickness dr and length L

Volume dV = (2πr)dr.L

∴ Strain energy stored in elemental volume dV is given by,

Case I: Strain energy in terms of torque

Case II: Strain energy in terms of τ_max

Case III: Strain energy in hollow shaft in terms of τ_max

SHAFT SUBJECTED TO COMBINED BENDING MOMENT AND TWISTING MOMENT

When the shaft is subjected to combined bending moment and twisting moment, the maximum stresses induced in shaft are due to the combined effect of shear stress (τ) and bending stress (σ_b)

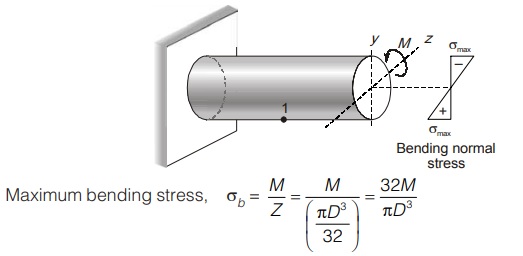
(i) Effect of pure bending

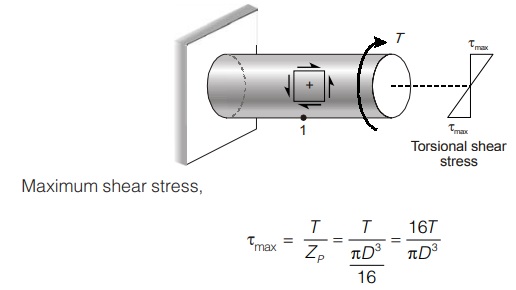
(ii) Effect of pure torsion

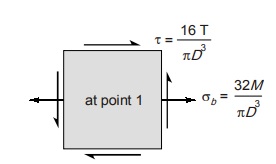
(iii) Combined effect of bending and twisting: 

Under the effect of bending moment (M) and torsional moment (T), the stresses at extreme bottom or top fibre construct a stress element as shown in figure.

Equivalent Bending Moment

It is that bending moment which produces same maximum normal stress as produced by combined effect of bending and twisting.
If M_e the equivalent bending moment. Then maximum normal stress produced will be

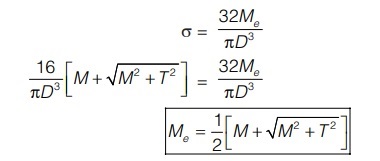
Equivalent Torque

It is that torque which produces same maximum shear stress as produced by combined effect of bending and twisting.
If T_e be the equivalent torque then maximum shear stress produced will be

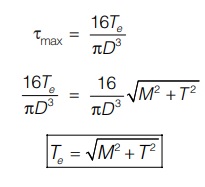
SHAFT SUBJECTED TO COMBINED AXIAL FORCE AND TORSIONAL MOMENT

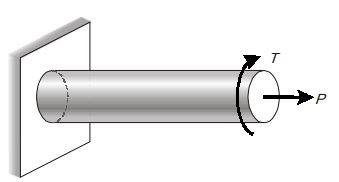
Consider a shaft subjected to an axial force and torsional moment as shown in figure.

Effect of axial force

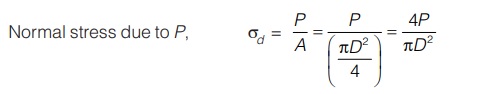
Effect of torsion

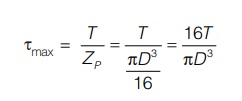
Combined effect of direct force and torsion

Consider any point on surface of shaft which will be in a state as shown below:
Therefore, principal stresses can be given as,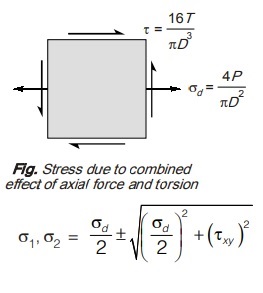

Elastic Instability and Critical Load

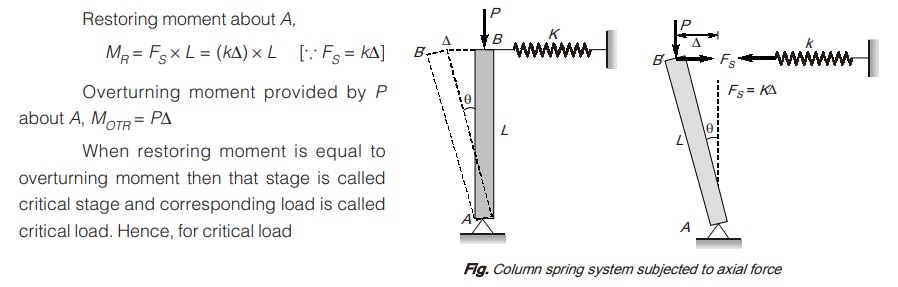
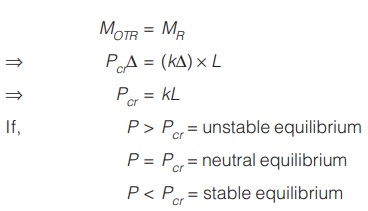
<< Previous | Next >>
Must Read: What is Strength of Material?