PRINCIPAL STRESSES AND MAXIMUM SHEAR STRESS

(a) Principal Stress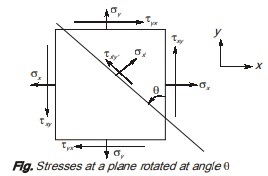

Consider a planar stress element subjected to normal and shear stress as shown below. Normal stress and shear stress on a plane inclined at an angle θ with vertical plane are represented by σ_x′ and τ_x′y′ as shown below.

When variation of normal and shear stress with angle of rotation θ is studied, it can be shown.

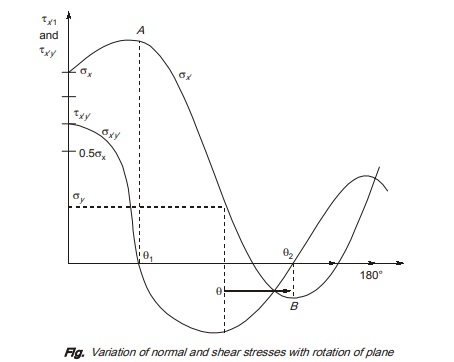
As we can see, when plane is rotated continuously in anticlockwise direction, normal stress at a point σ_x′ attains a maximum value and minimum value at point A and point B respectively known as major principal stress and minor principal stress represented by σ₁ and σ₂ respectively. It is to noted that when normal stress is maximum and minimum shear, stress is zero on these planes.

Expression For principal stresses:

σ_x’ = (σ_x + /2) + (σ_x – σ_y/2) cos2θ + τ_xy sin2θ ………(i)

As the principal stresses are maximum and minimum value of normal stress,

dσx′/dθ = 0 …….(ii)

dσ′/dθ = (σ_x – σ_y/2) – 2sin2θ + 2τ_xy cos2θ ………(iii)

tan2θ_P = 2τ_xy/σ_x – σ_y ……..(iv)

Angle θ_P defines the orientation of principal planes.
These are the planes on which principal stresses acts. From eq. (iv), θ_P has two values, one is from 0 – 90° and other is from 90° – 180°. Both value differ by a value of 90°

Hence, it can be inferred that on principal plane, the value of shear stress is zero.
• In uniaxial and biaxial stress element, principal planes are x and y plane themselves.
• In case of pure shear

MOHR’S CIRCLE

(a) For Plane Stress:

The transformation equation for plane stress are:

σ_x = (σ_x + σ_y/2) = (σ_x – σ_y/2) cos2θ + τ_xy sin2θ …..(i)

τ_{xy =} (σ_x – σ_y/2) sin2θ  + τ_xy Cos2θ ………(ii)

These equations can be represented in graphical form Known as Mohr’s circle. This method can be very helpful in determining the stresses on an included plane at point in body.
These equations are equation of circle in parametric form where angle 2θ is the parameter. Squaring both sides of equation and then eliminating the parameter by adding the equations.

we get.

(a) Construction of Mohr’s Circle
Sign convention

(i) Normal stresses: Tensile normal stresses are plotted in + s x direction.
Compressive normal stresses are plotted in –x direction.

(ii) Shear stress: 

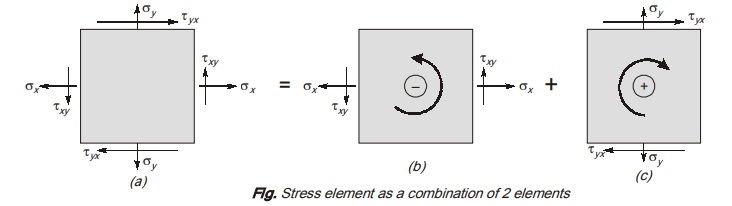
Stress element can be thought off as combination of two stress element as shown.
There is an anticlockwise moment about centre due to shear stress, so coordinates of this element are (σ_x’ –τ_xy) on Mohr’s circle.

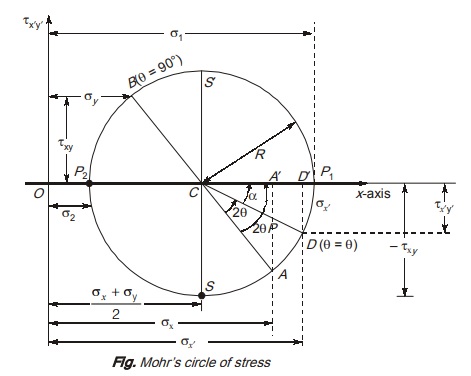
(a) Steps to construct Mohr’s circle for a plane stress element

Consider a planar stress element as shown in figures.

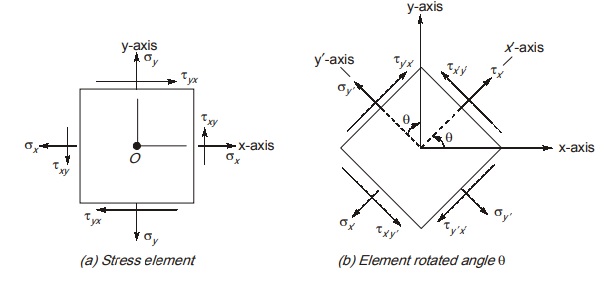
Steps:

1. Take σ’_x on x-axis and τ_x’y’ on y-axis as shown.
2. Locate the centre of circle having coordinate (σ_avg = σ_x + σy/2,0)
3. Locate a point A having coordinates (σ_x , σ_xy) representing the stress condition of x-face of stress element in figure a(1). [–ve sign with τ_xy is used as per our sign convention]
4. Locate a point B having coordinates (σ_y, τxy) representing the stress condition of y-face of stress element in figure a (ii). Line joining point A and B will pass through point C.

Radius of circle, R as derived earlier is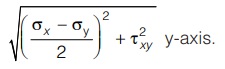

Thus a circle with centre C and radius R can be drawn in figure.
We have to determine stress on inclined face of element oriented, at angle θ as shown in figure a(ii) using Mohr’s circle method.

The point on Mohr circle corresponds to a plane at zero inclination i.e. at θ = 0
Take a point D on Mohr’s circle at angle 2θ in anticlockwise direction from radius CA. Point D has coordinates (σ’_x, – σ_x’y’).

Let α is angle between radius (i) and x-axis. Then from geometry.

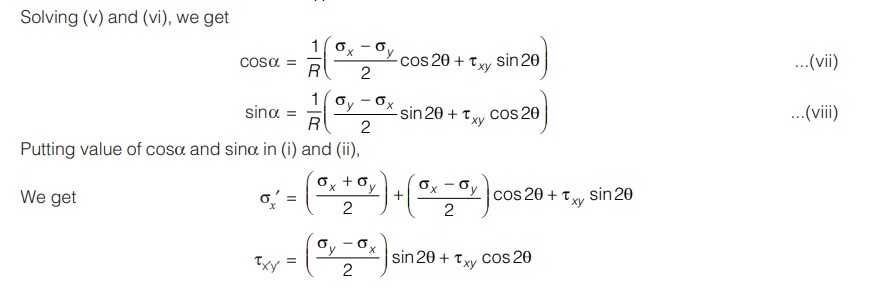
Which are same as equations for stress transformation.
Hence a point D on Mohr circle defined by angle 2θ represent the stress condition on x′ face of stress element, defined by angle θ.
Hence it can be said that when we rotate the stress element in anticlockwise direction by angle θ, the point on Mohr’s circle will be at angle 2θ in anticlockwise direction.

(b) Principal Stresses on Mohr’s Circle

In Mohr circle of stress figure cut the x-axis at two points namely P₁ and P₂. At these points, shear stresses are zero. Also, normal stress is maximum at point P₁ and minimum at point P₂. Hence these planes are principal planes and normal stresses on these planes are principal stresses.

Therefore, Coordinates of point P₁ = (σ₁, 0)
Coordinates of point P₂ = (σ₂, 0)
As stated earlier, angle between x-face of stress element and principal plane is θp₁, therefore angle between radius CA(θ = 0) and point P is 2θ_P.

(c) Maximum Shear Stress

We know that plane of maximum shear stress is at 45° to principal plane, therefore on Mohr’s circle, plane of maximum shear stress will correspond to point S and S′ which are at 90° to principal planes.

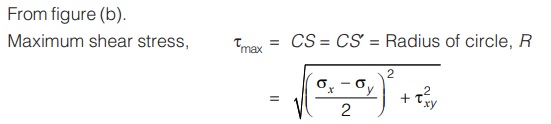
As derived earlier.
Hence, we can find stresses on any inclined planes, principal stresses, principal planes, maximum shear stress by constructing Mohr’s circle for stress element.

<< Previous | Next >>
Must Read: What is Strength of Material?