What is BMD in Strength of Materials?

Following points should be kept in mind during construction of loading diagram from the corresponding bending moment diagram.

1. If an inclined line uniformly varies between two sections, there will be no load between those two sections.
2. The BMD have parabolic curve for the member subjected to UDL.
3. The BMD have cubic curve for the member subjected to uniformly varying load.
4. If at a point concentrated moment M₀ acts then ordinate of BMD will be change by magnitude of M₀.
5. BMD is one degree higher than the SFD and two degree higher than the loading diagram.

ELASTIC CURVES USING BENDING MOMENT DIAGRAM

Elastic curve of a beam is axis of a deflected beam. Its equation for a beam subjected to loading can be derived using equation of bending.

Consider a simply supported beam of length L with overhang ‘a’ on both sides as shown in figure

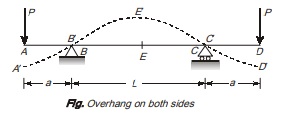
Dotted line in the figure shows deflection of beam ABCD at various points and thus curve A′B′E′C′D′ represents the elastic curve for beam ABCD.
Elastic curves of beams and frames can be drawn using BMD of beam.
Some points which are to be considered while drawing elastic curve are:

1. At hinged and roller support, deflection of beam is zero in vertical direction so deflection diagram or elastic curve ordinate at hinged support is zero but beam will have rotation at hinged or roller support.
2. At fixed support, deflection of beam is zero, so deflection diagram or elastic curve will have ordinate as zero and there will be no rotation at fixed end.
3. A positive bending moment tends to bend a beam or horizontal member concave upward as per our sign convention.
4. A negative bending moment tends to bend a beam or horizontal member concave downward per our sign convention.

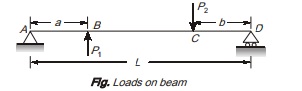
Its bending moment diagram is shown.

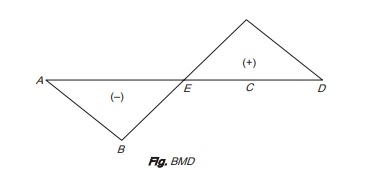
Its deflection curve is represented by curve A′B′C′D′as shown. Point ‘E’ represent inflection point on curve because in BMD at point C, bending moment changes sign from negative to point.

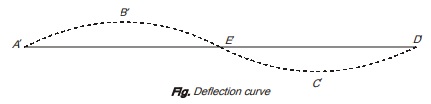
As the bending moment in portion AE is negative so shape of curve is concave downward and as the bending moment in portion ED is positive so shape of curve is concave upward in portion ED.

<< Previous | Next >>
Must Read: What is Strength of Material?