Hooke Law for Plane Stress

Consider a plane stress element is shown in figure.
In this stress element
σ_z = 0
σ_yz = 0
τ_xz = 0

Let the normal strains in x, y and z directions are represented by ε_x, ε_y, ε_z respectively.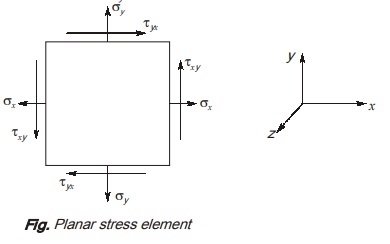

Shear strain in x-y plane, x-z plane, y-z plane are represented by φ_xy, φ_xz and φ_yz respectively.
As discussed in earlier chapters,

ε_x = σ_x/E – µσ_y/E …..(i)

ε_y = σ_y/E – µσ_x/E …..(ii)

ε_z = -µσ_y/E – -µσ_z/E …..(iii)

Normal strains in x, y and z directions can be found
out by using these equations if stresses are known.

Also, φ_xy = τ_xy/G

Note that axial stress σx and σy does not produce shear strain.
Solving (i) and (ii), we get

All the above 7 equations are known as Hooke’s law for plane stress.
In these equation,
E = Young’s modulus of elasticity
G = Shear modulus
µ = Poisson’s ratio

Volume Change

As discussed in earlier chapter

Volume strain for a body, ε_v = σ_x + σ_y + σ_z/E (1-2µ )

But for plane stress, σ_z = 0

So, dilatation or volumetric strain, ε_v = σ_x + σ_y /E (1-2µ )

For uniaxial stress, σ_y = σ_z = 0

So, volumetric strain, ε_v = σ_x /E (1-2µ )

Triaxial stress

Consider a stress element as shown in figure subjected to normal stresses σ_x, σ_y and σ_z only. As the stress element is subjected to axial stresses in three mutually perpendicular direction, it is said to be a case of triaxial stress.

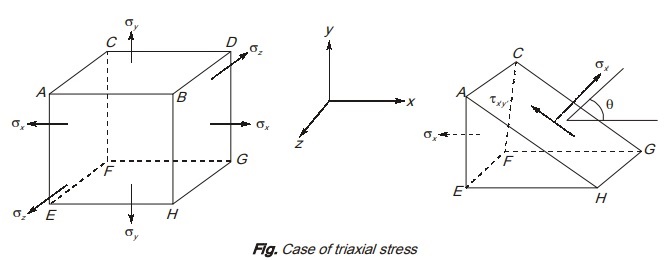
It is to be noted that as there are only normal stress on stress element and no shear stress, hence these normal stresses are principal stresses for the element.

Cut an inclined plane parallel to z-axis through element and normal to plane parallel to xy plane as shown in figure a(ii).

On face ACGH, only stresses are normal stress σx′ and shear stress τ_x′y′ which can be determined by using transformation equations. Note that these are independent of stress σ_z.

Thus, in triaxial state also, transformation equations or Mohr’s circle can be used to find normal and shear stress on an inclined plane.
Similar analysis can be done if planes parallel to x and y axis are cut.

Maximum Shear Stress

As studied earlier, plane of maximum shear stress occur at 45° to principal planes.
Hence, if we rotate the stress element about z-axis by 45°, the maximum value of shear stress,

(τ_max)_z = ± σ_x – σ_y/2 ——(i)

(τ_max)_y = ± σ_x – σ_z/2 ——(ii)

(τ_max)_x = ± σ_y – σ_z/2 ——(iii)

Absolute maximum shear stress is largest of shear stress obtained from above 3 equations.

Hooke’s law for triaxial stress

Let the strains produced by normal stresses on stress element in figure are ε_x,ε_y ,ε_z in x, y and z-axis respectively.

Volume change

As discussed in earlier chapters

Volumetric strains, εv = σ_x + σ_y+ σ_z /E (1 – 2µ)

Special case I: Spherical stress

A spherical stress element is a special type of triaxial stress in which

σ_x = σ_y = σ_z = σ_o

In this type of stress element, any plane inclined at an angle θ cut through the element will only have normal stress

σ_o and no shear stress.

The normal strain in all the direction is same. So, normal strain, ε = σ₀ /E (1 – 2µ)

Volumetric strains, εv = σ_x + σ_y+ σ_z /E (1 – 2µ)

σ_x = σ_y = σ_z = σ_o

ε = 3σ₀ /E (1 – 2µ) = 3ε₀

k = E / 3(1 – 2µ)

k = Bulk modulus of elasticity = σ_o/ε_v

 

Check More Links:
1. Specific Force in Open Channel Flow	2. What is hydrology in Civil Engineering?
3. What is a control section?	4. What is reciprocal ranging in surveying?
5. What is true bearing in surveying?	6. What are the advantages and disadvantages of using irrigation?
7. What is a compound curve in surveying?	8. What is the hydrologic cycle?