Euler Theory for Buckling Failure

The Swiss Mathematician Leonhard Euler in 1757 derived a formula for stability of long column. According to Euler’s theory, long columns fail in buckling only. This theory neglect the effect of direct stress induced in long column as compare to bending stress.

Assumptions of Euler’s Theory

1. Material is isotropic homogeneous and linear elastic in which Hooke’s law is valid.
2. Column is slender i.e., length of column is very large as compare to the cross-section dimension.
3. Column is long and prismatic i.e., EI is constant.
4. The axis of the column is perfectly straight when unloaded and load passes through the centroid of cross-section.
5. Column should be axially loaded.
6. Column fails only in buckling i.e., elastic bending.
7. Self weight of column is neglected.

Consider a column AB of length L with both ends A and B are hinged. Let P is critical load at which column is just buckled. Consider a section at a distance x from upper end B. Let y is the lateral deflection at section. Moment due to critical load P at section

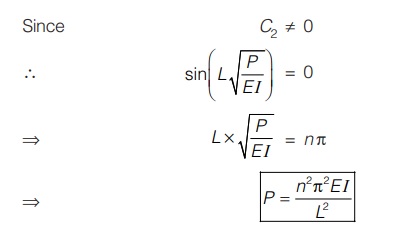where, P = Euler’s critical load
n = number of buckling loop
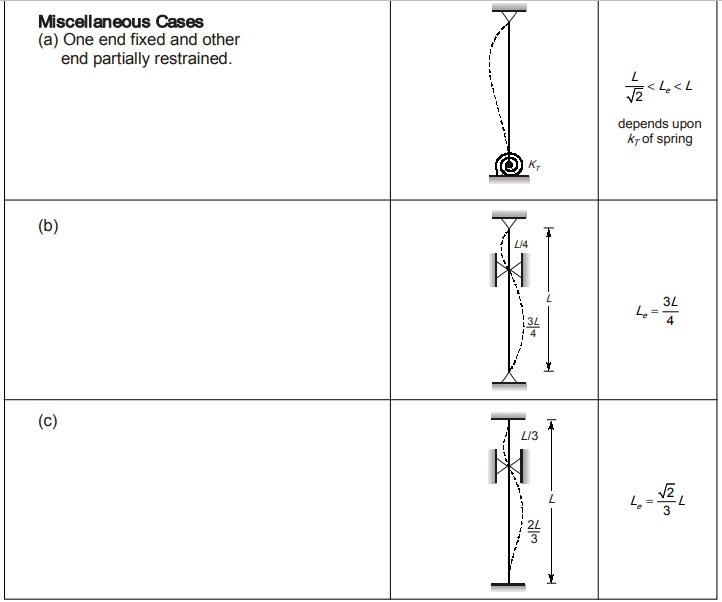
If failure is considered in basic mode then effective length of column should be used.

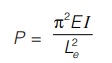
where, I = minimum moment of inertia ; L_e= effective length of column

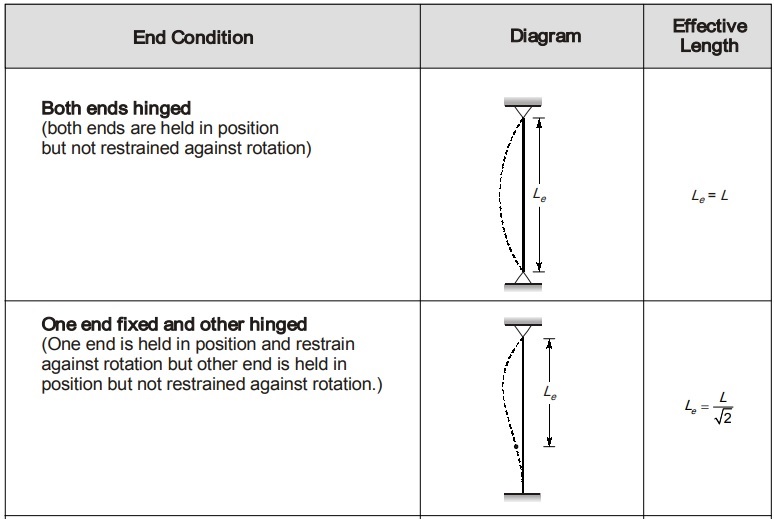
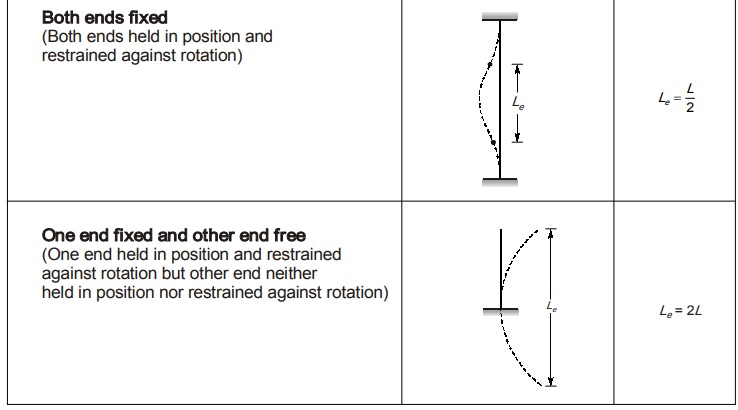
Effective Length of Column (L_e)

It is the distance between two consecutive points of contraflexure or between points of zero bending moment.

RANKINE’S GORDEN THEORY

This theory is commonly known as Rankine’s theory. Short column fails in crushing and long columns fails in buckling but in practice the columns fail due to combined effect of crushing and buckling. So this theory assumed combined (crushing and buckling) mode of failure. The Rankine’s critical load is given by

1/P = 1/P_c + 1/P_e

where, P_c = crushing load, P_e = Euler’s buckling load

Helical Spring

There are two types of helical springs:

(i) Closed coiled helical spring

In closed coiled helical springs, the wire or rod is wound closely in such a way that the pitch between two consecutive coil is very small. Closed coiled helical springs can be subjected to axial pull or axial twist.

Let spring is made of circular rod of length L, R is the mean radius of spring and d is diameter of rod from which spring is made. Also n is no. of turns in the spring.

Hence L = 2πRn

Let spring is subjected to axial force P which acts through the centre of spring. Hence due to force P, there will be a torque T = PR and shear force P on the section of metal rod. Let A is inner surface of spring and B is outer surface of spring.

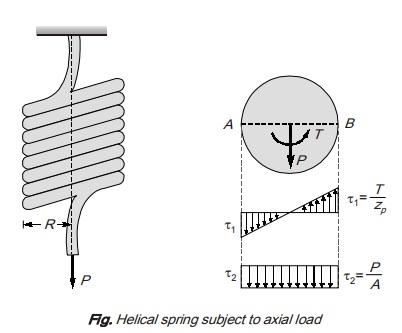
At the section of spring shear stresses are produced due to torque and shear force. Let shear stress due to torque is τ₁ and average shear stress due to shear is τ₂

Resultant shear stress at,

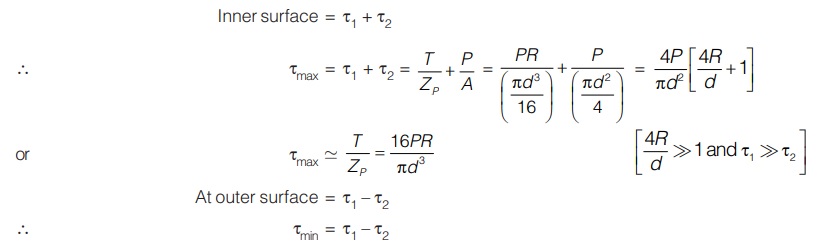
Strain energy stored in closed coiled spring

The strain energy stored in closed coiled helical spring will be due to torsion only.

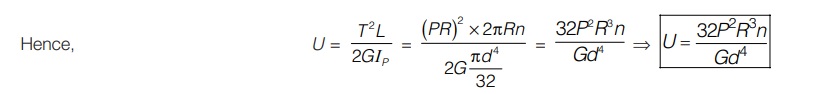
The axial deflection of spring under load P

According to Castigliano’s theorem

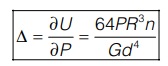
Stiffness of closed coil spring

The load required to produce a unit deflection in a spring is called stiffness of spring. If stiffness of spring k is coefficient of stiffness of spring

<< Previous | Next >>
Must Read: What is Strength of Material?