Composite Beams

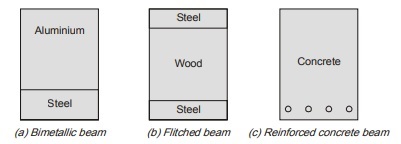
A beam that is built from more than one material is known as composite beams. Example are bimetallic
beams, flitched beams and reinforced concrete beam as shown.

The materials in composite beam can be:

(a) Simply placed over one another
(b) Rigidly connected

a) Simply placed over one another

Consider a beam section in which two different materials (1) and (2) are used to make the section with their Young’s modulus of elasticity E1 and E2 respectively. There is no bond between material (1) and (2) so they will bend independently about their own neutral axis and their stress distribution diagram is shown in figure.

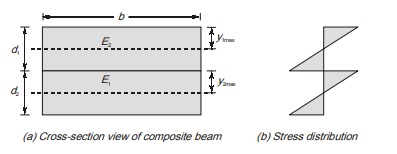
However, it is assumed that radius of curvature at junctions of both the materials is same So, R1 = R

From flexure formula, R = Ey/σ

(b) Rigidly connected

When different materials are rigidly connected to make the cross-section, then there is a common neutral axis and they behave like a single beam. But the position of neutral axis will not be the centroid of section because materials are different so the assumption of homogeneity does not apply here.
However, if by any method, section is converted in terms of any one material, then neutral axis will coincide with the centroid of equivalent section. In such types of beam bending strain diagram is linear hence strain in two material at a given vertical distance from NA will be same which is called strain compatibility condition. To convert one section into other, concept of modular ratio is used which is defined as ratio of modulus of elasticity of both the materials. In this method, width of one material is multiplied by modular ratio. Thus two types of method that can be used to analyse composite beam in which materials are rigidly connected are illustrated below with the help of analysis of flitched beam.

FLITCHED BEAM

Top and bottom flitched beam

Method-1

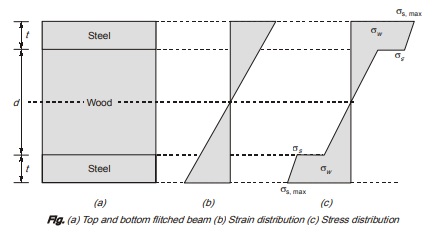
By strain compatibility; strain in steel = Strain in wood

ε_s = ε_w

σ_s/E_s = σ_w/E_w

σ_s/σ_w = E_s/E_w = m (modular ratio)

At same level, if stress in steel is σ_s, then corresponding stress in wood will be

σ_w = σ_s/m

σ_s = mσ_w

Let permissible stress in wood is σ_w
Permissible stress in steel is σ_s’max
Stress in steel at junction of wood is σ_s
Then, moment of resistance of wood section,

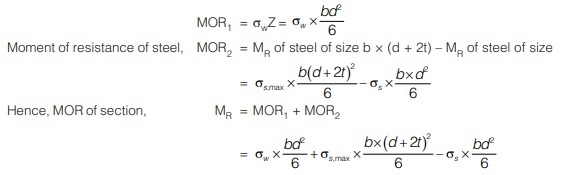
Method-2
Moment of resistance of top and bottom flitched beam can be calculated by converting heterogeneous section into either equivalent wooden section or steel section as shown in figure.

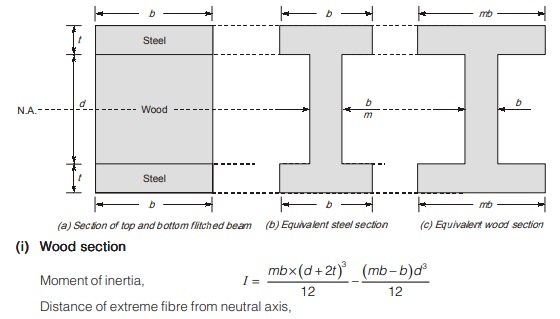
Side flitched beam

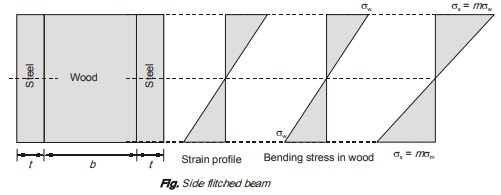
Moment of resistance of wood, MOR_w = σw x bd²/6

Moment of resistance of steel, MORs = σs x 2td2/6

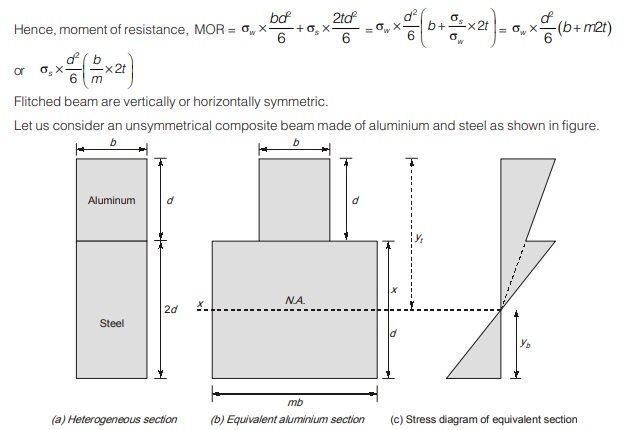
Modulus of elasticity of aluminium = E_a
Modulus of elasticity of steel = E_s

Modulus ratio, m = E_s /E_a

Let the heterogeneous section is converted into equivalent aluminium section by multiplying width of steel section by modulus.

Permissible stress in aluminium = σ_a
Permissible stress in steel = σ_s

First of all, we have to find moment of inertia of equivalent aluminium section about its neutral axis.

Location of neutral axis from top = ∫ydA/∫dA

After calculating location of neutral axis, let the moment of inertia calculated is I.

Let, the distance of top and bottom fibre of equivalent aluminium section from neutral axis is y_t and y_b respectively as shown.
Its section modulus will be different in tension and compression as the section is unsymmetrical.

Maximum stress at top of section = σ_a
Maximum stress at bottom of section,

Moment of resistance of section is taken as lesser of MOR₁ and MOR₂