Beam of Uniform Strength

For an economical design, the section of the beam may be reduced towards the support, as bending moment decreases towards the supports. The beam may be designed such that at every section, the extreme fibre stress reaches the permissible stress. A beam so designed is called beam of uniform strength this 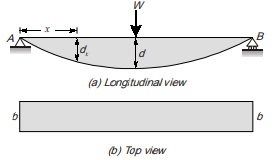can be done by.

(i) Uniform width varying depth
(ii) Uniform depth varying width

(i) Beam of constant width: Let width of beam is constant throughout the span, but depth of beam is variable, such that the depth of beam at a distance x from support A is d_x and at mid span it is equal to d.

Section modulus at a distance x from A is given by

Z_x = bd²_x/6

(ii) Beam of constant depth: Let depth of beam is constant throughout the span but width of beam is variable such that the width of beam at a distance x from support A is b_x and at mid span it is equal to b.

at a distance x from A, section modulus is given by

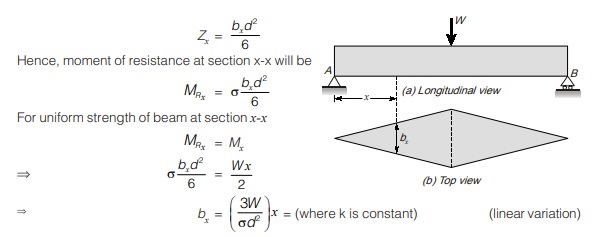
SHEAR STRESS IN BEAMS

Assumptions: 

1. Material is homogeneous and elastic.
2. Material obeys Hooke’s law.
3. Shear stress is assumed constant along width and variation is considered along depth of section. Consider a beam of rectangular cross-section of size b × d subjected to shear force V and two planes x₁-x₁ and x₂-x₂ are taken parallel to neutral axis. The direction of shear stress is assumed parallel to direction of  shear force as shown.

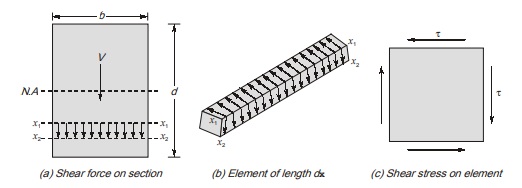
As we know that shear stress on one side of element is accompanied by complementary shear stress of equal magnitude acting on the perpendicular face on an element, hence equal horizontal shear stress will act on horizontal face as shown in figure (b).
Moreover, top and bottom fibres of beam can’t have horizontal shear stress, so vertical shear stress will also vanish at top and bottom of beam.

Variation of Shear Stress in Beam

Consider a small portion of length dx at a distance x from A between section x₁ and x₂. Let beam is subjected to uniformly distributed load of intensity w per unit run, which produces moment M at section x₁ and M + dM at section x₂. The portion above NA will be in compression and portion below NA .

Shear Stress Distribution in Rectangular Section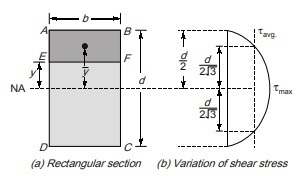

Consider a beam of rectangular section of width b and depth d as shown in figure.
Shear stress for an element at a distance y above NA is given by

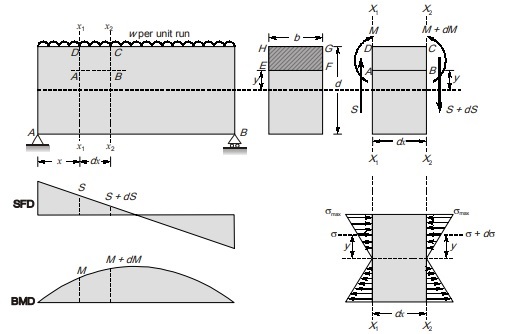
Let, M = bending moment at x₁-x₁
M + dM = Bending moment at x₂-x₂
S = Shear force at x₁-x₁
S + dS = Shear force at x₂-x₂
Consider an elementary strip at a distance y from the NA. Let σ is bending stress at section x₁-x₁ at a distance y from the NA and σ + dσ is at same location at section x₂ – x₂. By bending equation,

SHEAR CENTRE

Consider a singly-symmetric cross-section cantilever beam of length subjected to a downward concentrated load P.

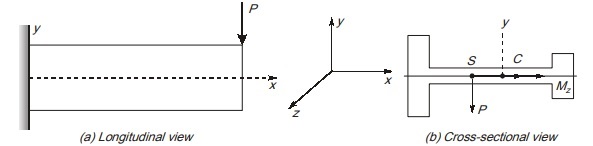
Its cross section i.e. I-section with unequal flanges is shown in figure (b). Due to action of load P at any section, two stress resultant exist:

(a) Bending moment M_z about z axis.
(b) Shear force V acting in y direction.

Bending moment M_z is resultant of normal stresses on cross-section while shear force V is resultant of shear stress. While deriving shear stresses, we have used variation of bending moment therefore distribution of shear stresses is affected by distribution of normal stresses.

Shear force should have its line of action passing through a point S lying on z-axis. This point S is known as shear centre and it does not coincide with centroid except in cases of doubly symmetric section.

If the resultant of shear stress i.e. shear force does not pass through shear centre, then section will be subjected to a torsional moment in addition to shear force, it can be said that a lateral load acting on a beam will produce bending without twisting only when it passing through shear centre.

PLANE STRESSES

Consider a rectangular stress element showing normal stress and shear stress on a point in a beam subjected to both bending and shear as shown in figure (a).

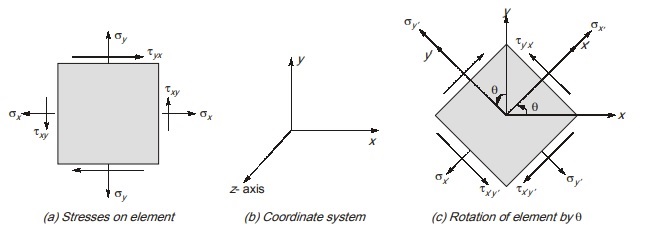
Right hand face of element is taken in positive x-direction. Similarly top face of element is taken in positive y-direction.

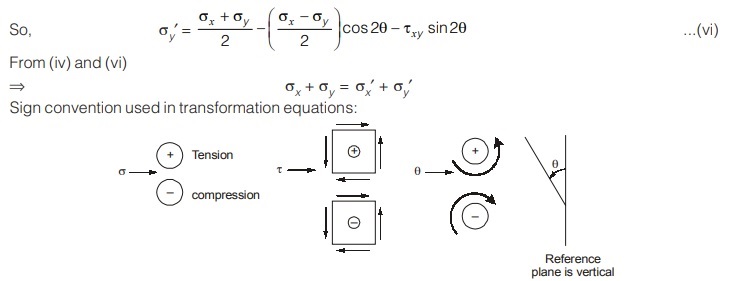
As, the element is subjected to stresses parallel to x and y axis, so it is a case of plane stress. As we know that shear stress on perpendicular plane is equal, therefore τ_xy = τ_yx

Now, the stress element is rotated through angle θ in anti-clockwise direction about z axis such that normals to right and top face are parallel to x′ and y′ axis.

Coordinate axes x′ and y′ will also be at angle θ to original x and y axis.

It is known as transformation of axes or stress transformation. Let the normal and shear stresses on rotated element are represented by σ_x′, σ_y′ , τ_x′y’ and τ_y′x’ respectively. Note that τ_x′y’ and τ_y′x’ are also equal in magnitude.

Stresses acting on rotated element can be expressed in terms of stress on original element using equations of static equilibrium. For this, consider a wedge shaped element as shown in figure below.

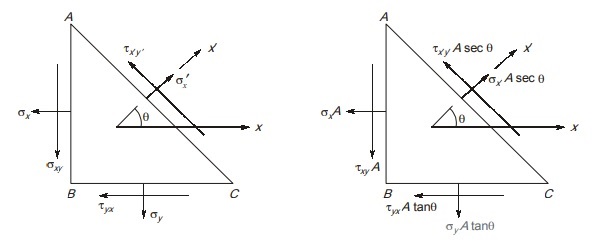
To use equations of static equilibrium, we need to rewrite stresses on rotated element in terms of forces acting on the faces of element. In, the figure, A is the area of face AB on which normal and shear stresses are acting. Then area of face BC will be A tanθ and area of face AC will be A secθ

By equations of static equilibrium ΣF_x = 0

σ_x′Asecθcosθ – τ_x′y’Asecθsinθ – σ_xA – τ_yxtanθ = o

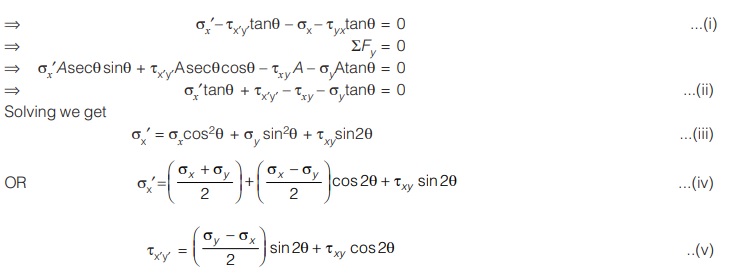
The equation for σ_x’ and τ_x′y’ are known as transformation equations.
Normal stress σ_y’ acting on a plane normal parallel to y′-axis is calculated by putting (90 + θ) in place of θ in eq. (iii).

Special Case:

(a) Uniaxial Stress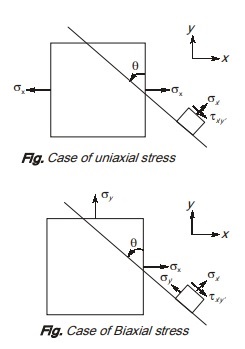

If an element xy is subjected to normal stresses in one direction only without shear stress then it is a case of uniaxial stress. Putting σ_y and τ_xy equals to zero in eq. (iv) and (v), we get,

Normal stress on plane rotated at angle θ, σ_x’ = σ_x cos2 θ.
Shear stress on plane rotated at angle θ, τ_x′y’ = –σ_x sinθ cosθ.

(b) Biaxial stress

If an element is subjected to normal stress in both x and y direction without shear stress, then it is a case of biaxial
stress.

Putting τ_xy equals to zero in eq. (iv) and (v), we get Normal stress on plane rotated at angle θ,

σ_x’ = (σ_x + /2) + (σ_x – σ_y/2) cos2θ

Shear stress on plane rotated at angle θ, τ_x′y’ = (σ_x – σ_y/2) sin2θ