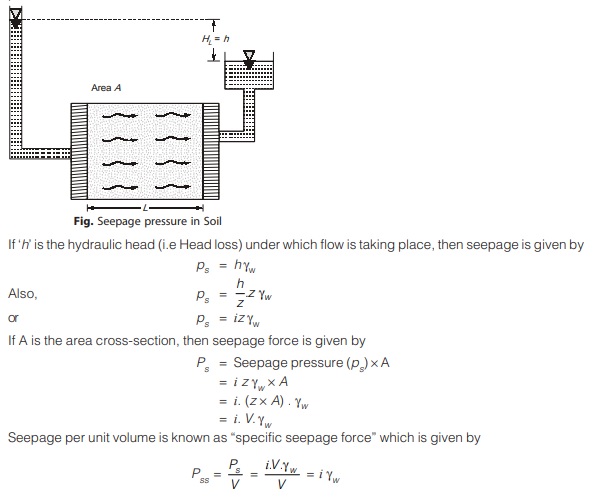
Seepage Pressure

• When water flows through saturated soil mass, the head available is dissipated as viscous friction, producing a frictional drag in the direction of flow on the soil particles. This drag force results in seepage force on soil mass which acts in the direction of flow.
  Hence, seepage pressure is the pressure exerted by the water over the soil solids through which it percolates.

QUICK SAND CONDITION

For upward flow condition, effective stress at any point within the soil mass is given by

It is clear from above equation that upward seepage pressure decreases effective stresses in the soil mass.

• If the seepage pressure is such that it equals the submerged weight of the soil mass, then effective stresses at that location reduces to zero. Under such condition, cohesionless soil mass losses all shear strength. Now soil mass has a tendency to move along the flowing water in the upward direction.
• This process in which soil particles are lifted over along with water is called quick sand condition. It is also known as ‘boiling of sand’ as the surface of sand looks it is boiling.
• At quick sand condition, net effective stress is reduced to zero. i.e.

• The hydraulic gradient under which quick sand condition occurs is termed as critical hydraulic gradient.
  If void ratio and specific gravity of soil is known, then i_cr may be given as

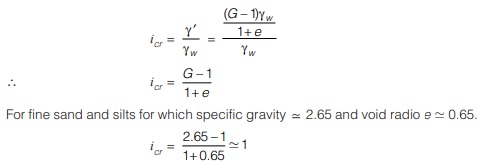
• At quick sand condition, cohesionless particles of fine sand may start flowing with the water which may result in piping failure below the hydraulic structure.
• In order to prevent quick sand or piping failure, the hydraulic gradient should be less then critical hydraulic gradient. Hence factor of safety against quick sand failure or piping failure is

FLOW NETS

The entire pattern of flow lines and equipotential lines is referred as a flow net. It is the graphical solution of Laplace’s equation for relevant boundary conditions. Thus, a flow net is a graphical representation of the head and direction of seepage at every point.

Properties of Flow Nets

• Flow lines (ψ-lines) and equipotential (φ-lines) meet each other orthogonally.
• Flow lines and equipotential lines are smooth continuous curves, being either elliptical or parabolic in shape.
• Area bounded between two adjacent equipotential lines and adjacent flow lines is referred to a flow field,
  which many be linear or curvilinear.
  • For isotropic medium, flow field is approximately square.
  • For non-isotropic medium, flow field is rectangular.
• Flow net remain unchanged if boundary conditions are not altered i.e flow net remain same for the same set of boundary conditions.
• Discharge through each flow channel is constant i.e., ∆q₁ = ∆q₂ = ∆q₃ = ∆q₄.

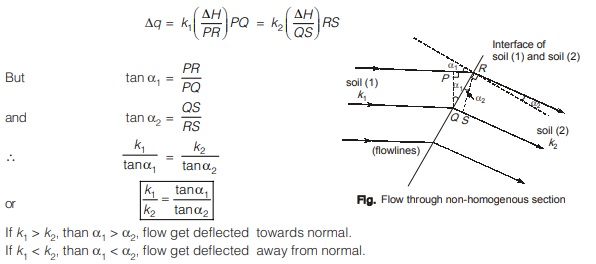
FLOW THROUGH NON-HOMOGENEOUS SECTION

• If there is a change in soil conditions, the flow lines are deflected at the interface of the soil with varying permeability, k₁ and k₂.
• Let the potential drop from P to Q and from R to S be ∆H, then