Irrigation Efficiencies

Efficiency is ratio of water output to water input. If losses will be more, then efficiency will be less. Various type of irrigation efficiencies are defined below:

Irrigation Requirements of Crops

Irrigation requirement of crops is the quantity of water, exclusive of rainfall, required by a crop in a given time period for their normal growth under field condition. It includes evapotranspiration not met by the rainfall. It also includes surface run off and percolation losses (these losses are unavoidable losses). Irrigation requirement of crops can be categorized under the following categories:

Consumptive Irrigation Requirement (CIR)

Consumptive irrigation requirement (CIR) is the amount of irrigation water that is required to meet the evapotranspiration (consumptive use) needs of a crop during its full growth.

CIR = C_u – R_e

where,

C_u = Consumptive use of water

R_e = Effective rainfall during growth period of crop

Net Irrigation Requirement (NIR)

Net irrigation requirement (NIR) is the amount of irrigation water required to be delivered at the field to meet the evapotranspiration needs of crop as well as other needs like leaching, presowing requirements etc.

NIR = CIR + LR + PSR

where,

LR = Leaching requirement

PSR = Presowing requirement

Field Irrigation Requirement (FIR)

Field irrigation requirement is the amount of water required to meet the NIR plus the amount of water lost as surface runoff and deep percolation.

 

FIR =NIR/n_a

where,

n_a = Water application efficiency

Gross Irrigation Requirement (GIR)

Gross irrigation requirement is the amount of water required to meet the FIR plus the amount of irrigation water lost in conveyance through canal system by evaporation and seepage.

Bed Formation from Practical Aspect

Bed of channel can attain various shapes depending upon velocity of water or discharge. When the velocity of flow is very less, then there is movement of particles on channel. Depending upon the velocity, channel can be in any shape as discussed below:

When velocity is gradually increased, then a stage comes when particles just start to move. It is known as threshold stage as discussed earlier. When velocity is further increased, bed develops ripples of saw-tooth type like in sand of any beach.

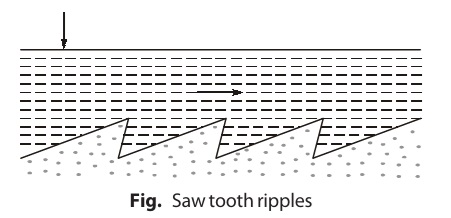
If the velocity starts increasing further, large periodic irregularities known as Dunes are developed on bed. During their first appearance, ripples are also superimposed on them.

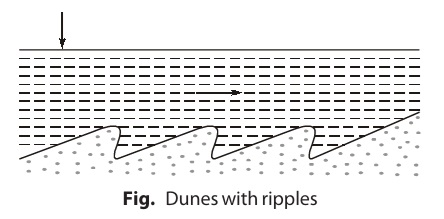
Now, if velocity is further increased, then only dunes are left on bed without ripples. It is to be noted that flow remains sub-critical till this stage.

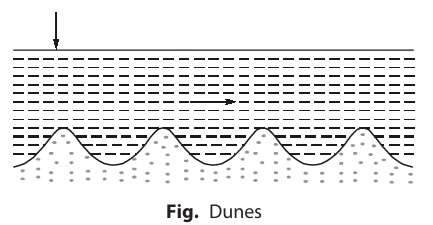
Further, increase in velocity, erases the dunes on bed leaving virtually a flat surface with sediment particle in motion.

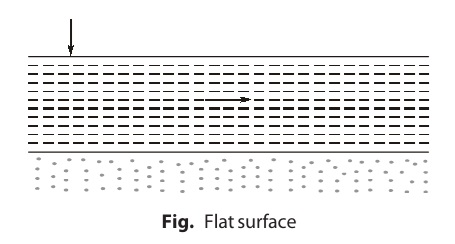
In next stage, increase in velocity results in formation of sand waves along with surface waves.

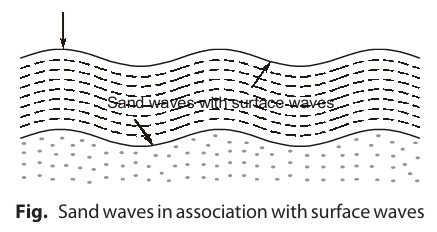
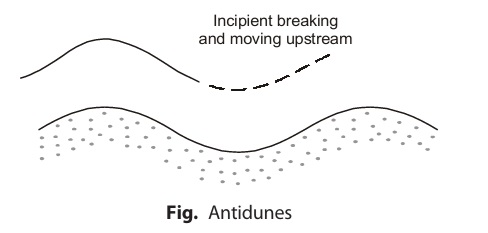
Further increase in velocity makes the flow super-critical from sub-critical and Froude number exceeds unity.
Surface waves becomes so steep that they break intermittently and move upstream while sediment particles moves in downstream direction. These waves are then known as anti-dunes.

Comparison of Lacey’s and Kennedy’s Theories

Lacey’s theory	Kennedy’s theory
1. Only one regime section for given discharge and silt factor.	There can be as many sections for the given discharge.
2. Did not leave silt grade as guess work but correlated silt factor f to diameter of silt and rugosity coefficient.	Simply stated CVR varied according to the silt grade but did not give any method to measure CVR.
3. Discarded arbitrary factors and gave general regime equation independent of rugosity coefficient, viz. V = 10.8 R 2/3S1/3	Gave no equation for regime velocity. Adoption of Kutter’s N and Chezy equation to work out mean velocity incorporated the limitations of those relations.
4. Considered hydraulic mean depth R as relevant variable and derive velocity formula in terms of R :	Considered depth as variable and gave critical velocity formula in terms of depth D.
V = 0.639 (fR)1/2	V0 = 0.55 mD0.64.
5. Specified regime slope for the given discharge and silt factor	Did not specify regime slope.
6. Silt is kept in suspension by vertical components of eddies caused by friction against wetted perimeter.	Eddies rise on account of roughness of bed and work up against depth. The eddies generated from sides are ignored.
7. Considered channel section semi-elliptical.	Considered channel section trapezoidal.
8. Section is wider and shallower.	Section is tighter and deeper.
9. Considered that channels cannot be in true regime and classified them into initial and final regime.	Considered all channels in regime when they neither silt nor scour.
10. Applicable to irrigation channels and rivers as well.	Applicable to irrigation channels only.

<< Previous | Next >>
Must Read: What is Irrigation Engineering?