Transition Curves
When a vehicle is moving on a straight road, it experiences zero centrifugal force because centrifugal force on a vehicle moving on a curve is inversely proportional to radius of curvature and radius of curvature of a straight road can be considered as infinity. Now, suppose it is to negotiate a horizontal circular curve of radius R.
Therefore, centrifugal force on vehicle = mv2 / R
where, m = mass of vehicle
v = velocity of vehicle
Therefore, it can be interpreted that vehicle was experiencing zero centrifugal force when it was moving on straight road and now a centrifugal force is acting on vehicle in outward direction. To make this transition smooth and safe for vehicles, a curve known as transition curve is provided between straight road and circular curve. Due to this transition curve, radius of curvature decreases from a value of infinity to radius of curvature of circular curve, R gradually. The rate of change of radius of curvature of transition curve depend upon shape of curve adopted and equation of curve.
Main objectives of transition curves can be listed as follows :
(a) To increase centrifugal force on vehicle from zero on straight road to some value say F on circular curve. (i.e. to introduce centrifugal force gradually).
(b) To decrease radius of curvature from infinite on straight road to its minimum value R at starting of circular curve.
(c) To increase superelevation and extra widening gradually from zero value on straight road to their full values on circular curve.
(d) To improve aesthetic appearance of road.
The ideal shape of a transition curve should be such that rate of introduction of centrifugal force or rate of change of centrifugal acceleration should be constant. For this condition to be fulfilled, the shape of transition curve should be such that radius of transition curve constantly decrease from infinite value at end of straight road to radius R of circular curve at end of transition curve. Hence, ‘spiral transition curve’ is ideal shape for transition curve because it fulfills all the conditions.
Different Types of Transition Curves
The different types of curve that can be adopted as shape of transition curves are :
(a) Spiral
(b) Lemniscate
(c) Cubic parabola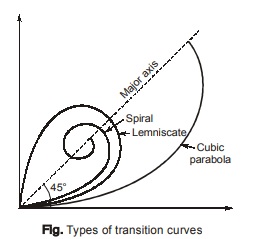
General shapes of these three curves are shown in figure. All the 3 curves follow almost the same path upto deflection angle of 4° and practically there is no significance even upto 9°. The characteristics of these curve is that their radii decreases as length increases. But rate of change of radius and consequently rate of change of centrifugal acceleration is not constant in case of lemniscate and cubic parabola, especially at higher deflection angles. In spiral curves, radius decreases constantly as length increases. Hence, it is recommended shape for transition curve by IRC. Another reason for spiral shape being adopted as transition curve is geometric property of spiral which makes calculation and setting of transition curve very easy.
Equations of Transition Curve
Consider a transition curve introduced between a straight road and circular curve as shown in figure below :
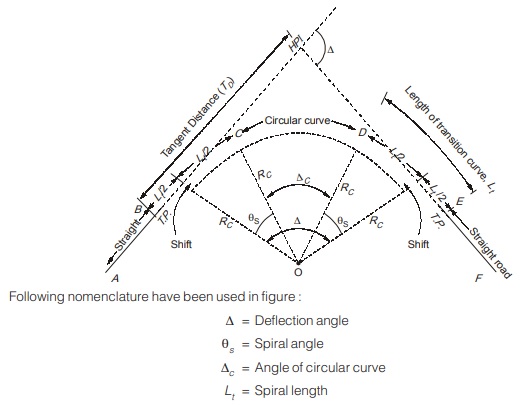
Rc = Radius of circular curve
T.D. = Tangent distance
HPI = Horizontal point of intersection
B = Beginning of spiral
E = End of spiral
C = Beginning of circular curve
D = End of circular curve
Some of properties of spiral curve are given below :

<< Previous | Next >>
Must Read: What is Highway Engineering?

