Length of Summit Curve

For summit curve, the most important consideration in determining length of curve is requirement of sight distance. Length of summit curve depends on whether sight distance is lesser or greater than length of curve.

Length of summit curves for both cases are given below

Case 1 : Consider a summit curve as shown in figure below.

(a) If stopping sight distance, i.e., SSD is used as a sight distance, then
h₁ = 1.2 m and h₂ = 0.15 m.
Putting the values in above equation, we get

Ls = NS² / 4.4

(b) If overtaking or intermediate sight distance, i.e., OSD or ISD is used as a sight distance, then
h₁ = 1.2 m, h₂ = 1.2 m.
Putting values in above equation, we get

Ls = NS² / 9.6

Case 2 : When length of curve is less than sight distance S provided on the road.

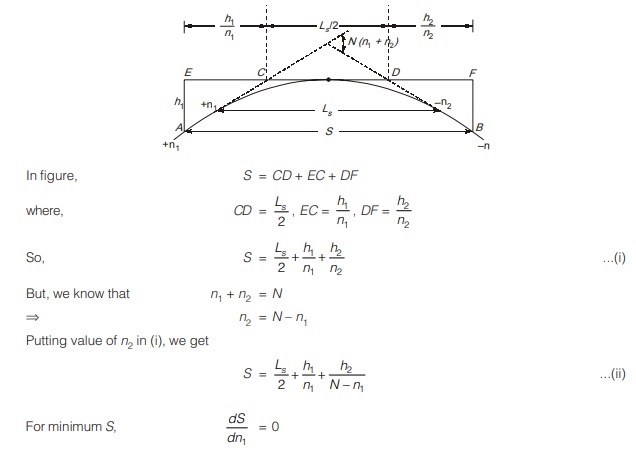
(a) If stopping sight distance is provided on road, then h1 = 1.2 m, h2 = 0.15 m. Putting values in eqn. (iv), we get

Ls = 2S – 4.4/N

(b) If overtaking or intermediate sight distance, i.e., OSD or ISD is provided on road, then h1 = 1.2 m, h2 = 1.2 m. Putting values, we get

Ls = 2S – 9.6/N

Length of Valley Curve

These curves are designed mainly to serve two criteria :

(a) Allowable rate of change of centrifugal acceleration.
(b) The required head light sight distance for night driving.

Length of valley curve is calculated on basis of both the criteria and higher length is adopted as length of valley curve.

Hence, shape of valley curve is chosen as combination of transition curve. Two similar transition curves of equal length (without circular curve in between) where, Lt = Lv /2, having radius R at common point of meeting of transition curves are adopted as valley curve.

(a) Length of valley curve as per comfort condition

Length of transition curve so as to provide a limit on the rate of change of centrifugal acceleration, Lt is given by

It is to be kept in mind that minimum radius of curvature of transition curve, R is given by, R = Lt / N
where Lt = length of transition curve.
So, minimum radius of valley curve,

R = LV / 2N

where, LV = Length of valley curve

(b) Length of valley curve based on head light sight distance : 

Length of valley curve based on headlight sight distance is calculated in the following two cases :

Case-1: When length of valley curves, LV is greater than stopping sight distance SSD

It is assumed that length of valley curve LV is greater than headlight sight distance which is at least taken equal to stopping sight distance. To calculate length of valley curve, consider a valley curve

which is assumed to be parabolic in shape having equation y = ax² where a = N / 2L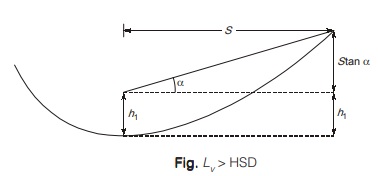

From figure, we can say that available sight distance for vehicle will be minimum when it is at lowest point on curve. So, while calculating required length of curve, vehicle is assumed to be on lowest point so that the calculated length of curve is sufficient for vehicle when it is not on lowest point.

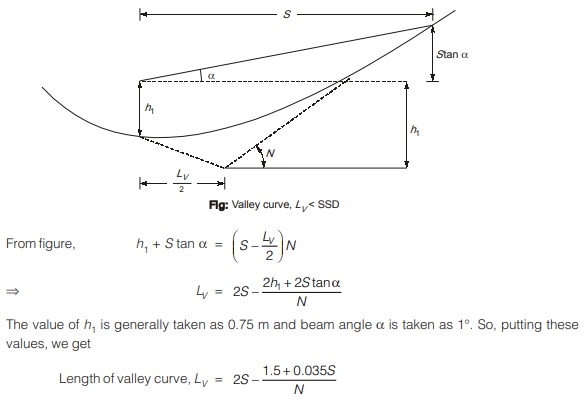
Case-2: When length of valley curve is lesser than stopping sight distance SSD

Here, length of valley curve is less than available sight distance. To calculate length of valley curve, consider a valley curve of parabolic profile with vehicle at starting of curve so that available sight distance for vehicle is minimum.

Lowest Point on Valley Curve

This point is located on curve to provide cross drainage to water. This point will be on bisector of angle between the grades, if the curve is symmetrical.
When the valley curve is unsymmetrical, then lowest point lies on flatter grade, and this point is X_o distance from starting point, i.e., first tangent point of curve.

X_o = L √n₁/2N

It is obtained by assuming the curve to be of cubic parabola profile.

<< Previous | Next >>
Must Read: What is Highway Engineering?