Viscosity

What is Viscosity in fluid mechanics?

Viscosity is the property of fluids by virtue of which they offer resistance to shear or angular deformation.

It is primarily due to cohesion (in case of liquids) and molecular momentum exchange (in case of gases) between fluid layers, and as flow occurs, these effects appear as shearing stresses between the moving layers.

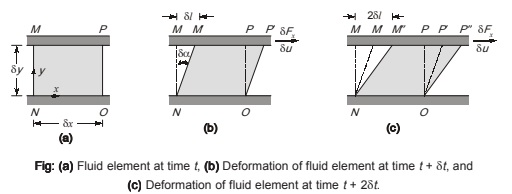
Consider a fluid element between the two infinite plates. The rectangular fluid element is initially at rest at time t. Let us now suppose a constant rightward force δF_x is applied to the upper plate so that it is dragged across the fluid at constant velocity δu. The relative shearing action of the plates produces a shear stress, τy_x , which acts on the fluid element and is given by

where δAyis the area of contact of the fluid element with the plate and δF_x is the force exerted by the plate on that element.
Various positions of the fluid element, illustrate the deformation of the fluid element from position MNOP at time t, to M′NOP′ at time t + δt, to M″NOP″ at time t + 2δt, due to the imposed shear stress. The deformation of the fluid is given by

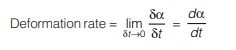
Distance between the points M and M′ is given by,

Thus, the rate of angular deformation is equal to velocity gradient across the flow.

Newton’s law of viscosity

According to Newton’s law of viscosity, shear stress is directly proportional to the rate of deformation or velocity gradient across the flow.

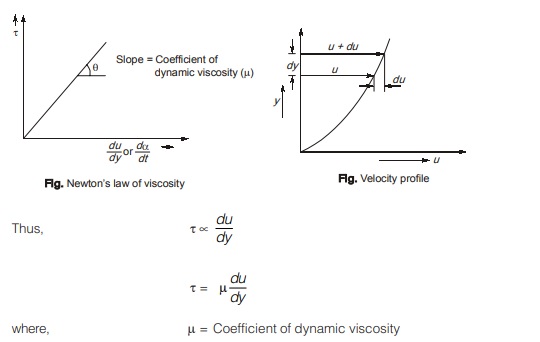
Dynamic Viscosity (µ)

• Dimension of µ = [M L^–1 T^–1]
• Unit of µ = Ns/m² or Pa.s
• In C. G. S. units, µ is expressed as ‘poise’, 1 poise = 0.1 N-s/m²
• A 20°C and at standard atmospheric pressure, (µ)_water ≈ 10^-3 Ns/m²;
(µ)_air ≈ 1.81 × 10^-5 Ns/m²

Kinematic Viscosity (ν)

• The kinematic viscosity (ν) is defined as the ratio of dynamic viscosity to mass density of the fluid.
Therefore, ν = µ/ρ
• Dimension of ν = [L² T^-1]
• Unit of ν = m²/s or cm²/s (stoke, in C.G.S. units)
• 1 stoke = 10–4 m²/s
• At 20°C and standard atmospheric pressure, νwater = 1 × 10^-6 m²/s, νair = 15 × 10^-6 m²/s

Variation of viscosity with Temperature

Dynamic viscosity: Increase in temperature causes a decrease in the dynamic viscosity of a liquid, whereas 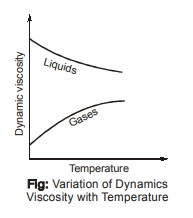viscosity of gases increases with temperature growth. The reason for the above phenomena is that; in liquids; viscosity is
primarily due to molecular cohesion which decreases due to increase in volume due to temperature increment, while in gases, viscosity is due to molecular momentum transfer which increases due to increase in number of collision between gas molecules.

Kinematic Viscosity: Kinematic viscosity is ratio of dynamic viscosity to the density of fluid. In case of liquids with increase in temperature, the dynamic viscosity as well as density both decrease but decrease in dynamic viscosity is very high as compared to density. So, overall kinematic viscosity will decrease for liquids. On the other hand, in case of gases, with increase in temperature dynamic viscosity increases and density decreases. So overall kinematic viscosity increases for gases.

Variation of viscosity with pressure

Dynamic viscosity: In fluids, dynamic Dynamic viscosity: viscosity is practically independent of pressure except at
extremely high pressure.
Kinematic viscosity: In Kinematic viscosity: liquids, kinematic viscosity is independent of pressure at low to moderate pressure.
In case of gases, density increases with increase in pressure, therefore kinematic viscosity decreases.

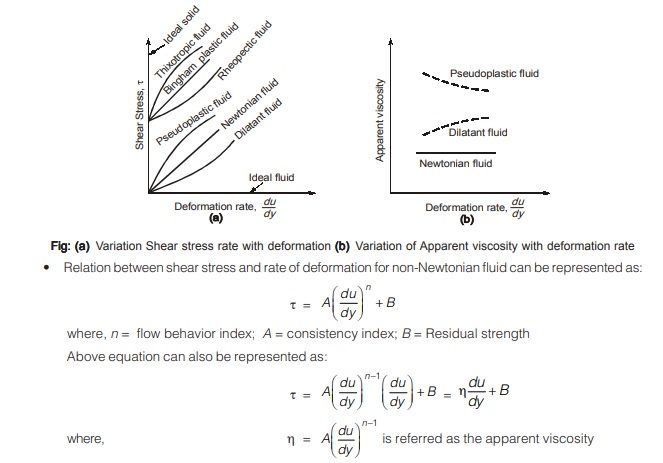
Types of Fluids

The fluids are classified into following types based on shear stress variation with velocity gradient:

Newtonian Fluids

• Fluids which obey newton’s law of viscosity are known as Newtonian fluids.
• General relationship between shear stress and velocity gradient is given by

τ = A (du/dy)ⁿ + B

• For Newtonian fluids, n = 1, A = µ and B = 0,

τ = µ du/dy

Examples: Air, water, Mercury, Petrol, Kerosene, etc.

Non-Newtonian Fluids

• Fluids for which shear stress is not directly proportional to deformation rate are Non-Newtonian fluids.
  Examples: Toothpaste and paint.
• Non-Newtonian fluids are commonly classified as having time-independent or time-dependent behavior.

LIVE SSC-JE Practice Programme | Fluid Mechanics

<< Previous | Next >>
Must Read: What is Fluid Mechanics?