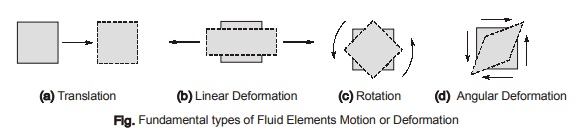
Types of Motion or Deformation of Fluid Elements

A fluid particle as it moves can undergo the following four types of displacement viz,

1. Linear Translation or Pure Translation
2. Linear Deformation
3. Rotation
4. Angular Deformation

• Linear Translation: The movement of a fluid element in such a way that it moves bodily from one position to another position.
• Linear Deformation: The deformation of a fluid element in linear direction when the element moves. In this, the axes of the element in the deformed position are parallel with that of in undeformed position but, their length changes.
• Rotation : The movement of a fluid element in such as way that both of its axes (horizontal as well as vertical) rotates in the same direction.

The rate of rotation or angular velocity of the fluid particle about any axis is defined as the average angular velocity of any two infinitesimal linear elements in the particle that are perpendicular to each other and to the axis of rotation.
Consider a fluid element PABC rotating d about z-axis at point P to new position PA′B′C′.

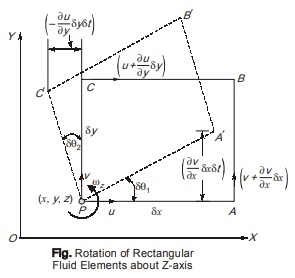
Angular Deformation or Shear deformation: The average change in the angle contained by two adjacent sides. Let, ∆θ₁ and ∆θ₂ be the change in angle between two adjacent sides of fluid element.

VELOCITY POTENTIAL

• The velocity potential (φ) is defined as a scalar function of space and time such that its negative derivative with respect to any direction gives the fluid velocity in that direction.
• Mathematically, velocity potential is defined as :
  In cartesian coordinate system:

φ = f (x, y, z, t) for unsteady flow
φ = f(x, y, z) for steady flow

STREAM FUNCTION

• The stream function (ψ) is defined as a scalar function of space and time, such that its partial derivative with respect to any direction gives the velocity component at right angle (in the counter clockwise) to that direction. This function is defined only in 2D i.e one plane.
• Mathematically, stream function may be defined as ψ = f(x, y, t) for unsteady flow and ψ = f(x, y) for steady flow.

If  ∇2ψ ≠ 0
∴ Rotational flow condition.
Hence, ψ exists in both rotational as well as irrotational flow.

• In terms of cylindrical polar coordinates

where, V_r and V_θ are the components of velocity in r and θ directions respectively.

• The Cauchy-Riemann equation in cylindrical polar coordinates may thus be expressed as

<< Previous | Next >>
Must Read: What is Fluid Mechanics?