Siphon

• A siphon is a long bent pipe which is used to carry water from a reservoir at a higher elevation to another 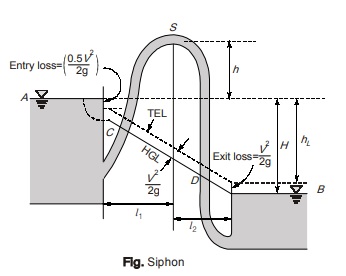reservoir at a lower elevation when the two reservoirs are separated by a hill or high level ground.
• The rising portion of the siphon is known as the inlet leg, the highest point is known as summit and the portion between the summit and the lower reservoir is known as outlet leg. The inlet limb of a siphon is usually smaller than the outlet leg.
• The length of siphon may be taken as the length of its horizontal projection. Hence, the HGL and the TEL may also be obtained in the same manner as in the case of an ordinary long pipe.
• HGL cuts the siphon at points C and D, so that some portion of the siphon is above the HGL.
• The vertical distance between the HGL and the centreline of the pipe represents the pressure head at any section. If the HGL is below the centreline then the pressure is negative or below atmospheric and if it is above the centreline then the pressure is positive or above atmospheric. Thus below points C and D the pressure is above atmospheric and above points C and D pressure is below atmospheric.
• The pressure is least at summit point which should not be less than the vapour pressure of liquid to avoid air lock formation at summit. (For water it is 2.5 m at 20°C).
• Atmospheric pressure of water is equal to 10.3 m of water. Therefore pressure at summit may be reduced upto –10.3 m of water (absolute vacuum). However in actual practice if pressure is reduced to about 2.5 m of water (absolute) dissolved gases start coming out of the solution and form an air – lock at summit. Therefore the siphon should be laid so that no section of pipe will be more than 7.8 m above the hydraulic grade line. Therefore, in order to limit the reduction of pressure at summit, the length of inlet leg is required to be limited. If long inlet leg is provided, loss of head due to friction will be more, resulting in further reduction of pressure at summit.
• Pressure at C and D = Atmospheric pressure
• If total head loss between A and B is H, then H = entry loss + friction loss + exit loss

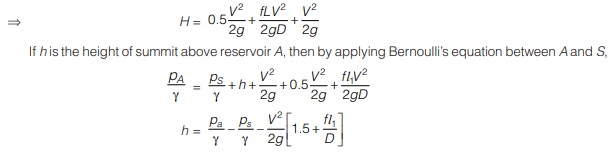
FLOW BETWEEN RESERVOIRS AT DIFFERENT LEVEL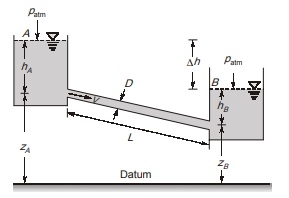

Consider the flow of water from one reservoir to another as shown in Figure. The two reservoirs A and B are maintained with constant levels of water. The difference between these two levels is ∆h.  Therefore water flows from reservoir A to reservoir B. Application of Bernoulli’s equation between two points A and B at the free surfaces in the two reservoirs give

<< Previous | Next >>
Must Read: What is Fluid Mechanics?