Shear Stress in Turbulent Flow

Shear stress at the boundary in case of turbulent flow, is much more than that in laminar flow. This is because at boundary velocity gradient is higher in case of turbulent flow than that in laminar flow.

The velocity fluctuation causes continuous interchange of fluid masses between layers which leads to transfer of momentum. This momentum transport causes additional shear  stresses of high magnitude.

Total shear stress in turbulent flow consists of laminar and turbulent shear. Thus, τ_Total = τ_Laminar + τ_Turbulent Following are the various theories for determination of shear stress in a turbulent flow.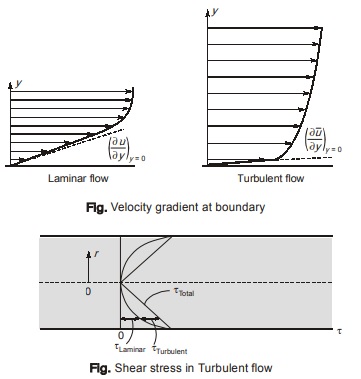

HYDRODYNAMICALLY SMOOTH AND ROUGH BOUNDARIES

• In case of turbulent flow in pipes, very close to the wall, effect of viscosity is maximum. Hence, it is said that a laminar sublayer exists near the boundary.
• The thickness of laminar sublayer is directly proportional to the kinematic viscosity and inversely proportional to flow velocity. Thus, thickness of laminar sublayer decreases with increase in Reynolds number.

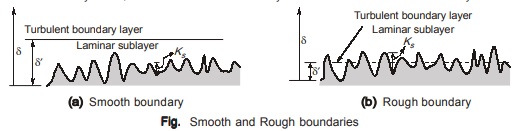
• lf thickness of laminar sublayer is large, and eddies are not able to penetrate upto the boundary, then boundary acts as hydrodynamically smooth. Boundary where as if thickness of laminar sublayer is small and eddies penetrate upto the boundary it is said to be hydrodynamically rough.
• A pipe boundary will behave as hydrodynamically smooth or rough depending upon the relative magnitude of average height of the surface protrusions (K_s) and the thickness of the laminar sublayer (δ′). Hence, (K_s/δ′) must be parameter which will determine whether a pipe boundary is hydrodynamically smooth or rough.

Loss of Energy due to Sudden Enlargement

• If the cross section of a pipe is abruptly enlarged at a certain place, the fluid emerging from the small pipe is unable to follow the abrupt deviation of the boundary. The streamline takes a diverging pattern. This creates pockets of turbulent eddies in the corners resulting in the dissipation of mechanical energy into intermolecular energy.
• Consider fluid of unit weight γ is flowing in a pipe whose area is enlarged at a section.
• The upstream pressure p₁ is lower than the downstream pressure p₂, since the upstream velocity V₁ is higher than the downstream velocity V₂ as a consequence of continuity equation.
• The fluid particles near the wall due to their low kinetic energy cannot overcome the adverse pressure hill in the direction of flow and hence follow up the reverse path under the favourable pressure gradient (from p₂ to p₁).
  This creates a zone of recirculating flow with turbulent eddies near the wall of the larger tube at the abrupt change of cross-section resulting in a loss of total energy p′ is the pressure in density of the liquid eddies on the area (A₂ – A₁).
  From Newton’s second law of motion
  p₁A₁ + p′(A₂ – A₁) – p₂A₂ = ρQ(V₂ –V₁)
  Pressure in the separation region is generally taken as p₁, i.e. p′ = p₁, then
  p₁A₁ + p′(A₂ – A₁) – p₂A₂ = ρQ(V₂ –V₁)
  (p₁ – p₂)A₂ = ρQ(V₂ –V₁)

Also, from Bernoulli’s equation,

<< Previous | Next >>
Must Read: What is Fluid Mechanics?